Gamma Hedging: Overview, Uses, Implementation, Example, Tools, Risks, Profitability

Gamma hedging is a strategy that reduces risk by controlling how quickly an option’s delta changes with movements in the underlying asset. Gamma hedging comes in where delta hedging alone neutralises directional exposure, but fails to account for the instability of delta as prices move.

Gamma, the second derivative of the option price with respect to the underlying, measures convexity. A trader holding short options faces adverse gamma exposure because delta shifts rapidly against them during sharp price swings. By gamma hedging, they attempt to stabilize delta fluctuations and create smoother P/L curves.

What Is Gamma Hedging?

Gamma hedging is the process of adjusting a portfolio to neutralize gamma exposure, ensuring delta remains stable even as the underlying price changes. It goes beyond delta hedging by addressing the curvature of the option’s sensitivity.

In formula terms

• Delta (Δ) = ∂Option Price / ∂Stock Price
• Gamma (Γ) = ∂²Option Price / ∂Stock Price² = ∂Δ / ∂Stock Price

A portfolio with zero delta but negative gamma will still experience rapid losses during volatile moves. Gamma hedging solves this problem by using additional options to offset curvature.

For example, a short straddle is short gamma. If the stock price moves sharply, delta quickly shifts against the position, leading to large losses. By buying additional options (often OTM or long-dated), the trader offsets this gamma risk, slowing down delta drift.

Gamma hedging is therefore not about betting on direction but about managing exposure to volatility and convexity.

How Does Gamma Hedging Work?

Gamma hedging works by rebalancing positions dynamically, so the portfolio remains delta-neutral as the underlying moves. This involves trading either the underlying asset or additional options to counteract delta changes caused by gamma.

The process follows three key steps

1. Measure Gamma Exposure – Calculate the net gamma of the portfolio. Short gamma positions (e.g., short straddles, iron condors) will require frequent hedging, while long gamma positions (long straddles, strangles) are naturally hedged by convexity.
2. Track Delta Drift – As the underlying price moves, gamma shifts delta. Example: A short ATM straddle on NIFTY has net delta = 0 initially, but as NIFTY rises, delta turns strongly negative due to negative gamma.
3. Hedge the Delta Dynamically – Use futures or underlying stock trades to rebalance back to delta-neutral. This often requires multiple adjustments within a day for high-gamma positions near expiry.

Formula for Hedge Adjustment

New Delta Exposure = Old Delta + (Gamma × Change in Price)

Hedge = – New Delta

Example: If a trader is short 2000 gamma and the stock moves up by 2 points, delta changes by +4000. To remain hedged, they short 4000 shares.

Thus, gamma hedging is essentially dynamic delta hedging with a focus on convexity.

Why Use Gamma Hedging Strategy?

Gamma hedging is used to reduce directional risk, stabilize option portfolios, and manage volatility-driven losses. It ensures delta neutrality remains intact even when prices swing sharply.

• Neutralizing Directional Bias – Short options have negative gamma, which amplifies losses during volatile moves. Gamma hedging protects against sudden market swings.
• Profiting from Time Decay – Market makers and option sellers use gamma hedging to hold short-gamma positions while collecting theta decay. The hedge offsets risk, allowing them to capture income from premium erosion.
• Volatility Management – Gamma hedging aligns exposure with expected volatility. If implied volatility spikes, hedged traders suffer less because their positions are structurally balanced.
• Portfolio Protection – Hedge funds and institutional traders use gamma hedging to control overall book risk, especially when dealing with large positions across multiple expiries.

Without gamma hedging, delta-neutral strategies often collapse during extreme price movements. With gamma hedging, risk is redistributed in a more controlled way, though at the cost of frequent adjustments.

When to Use Gamma Hedging?

Gamma hedging is most effective during high-gamma conditions such as near expiry, at-the-money strikes, or volatile event-driven periods. Traders adopt it when delta is highly unstable.

1. Short ATM Options Near Expiry – Gamma spikes sharply near expiry for ATM options, making delta extremely sensitive. Traders hedge aggressively to avoid blow-ups.
2. Event Risk (Earnings, Fed Meetings, Elections) – Before major events, implied volatility rises, and gamma increases as the market prepares for large moves. Gamma hedging helps mitigate sudden swings.
3. Long-Dated Structured Products – Banks running complex derivatives use gamma hedging to stabilize their books over months or years.
4. Illiquid Underlyings – In assets where spreads are wide, gamma hedging ensures traders do not take unintended directional bets.

For retail traders, gamma hedging is rarely practical due to cost. But for professional desks, it is indispensable during short-term volatility bursts.

Who Uses Gamma Hedging?

Gamma hedging is primarily used by institutional players such as market makers, prop desks, and hedge funds. These entities manage large exposures and cannot afford uncontrolled gamma risk.

• Market Makers – Continuously hedge gamma to provide liquidity while avoiding inventory blow-ups. They sell options but hedge aggressively to remain neutral.
• Hedge Funds & Volatility Traders – Use gamma hedging to run volatility arbitrage strategies, scalping profits from price oscillations while neutralizing directional risk.
• Banks & Structured Product Desks – For products like barrier options or exotic derivatives, gamma hedging ensures smooth book management.
• Sophisticated Retail Traders – Advanced retail traders with access to option analytics (via platforms like Strike, Sensibull, or Quantsapp) attempt gamma hedging during volatile periods.

How to Implement Gamma Hedge?

To implement a gamma hedge, you need to offset the risks of a short gamma position (like a short straddle) by adding long gamma exposure. Here’s a step-by-step breakdown.

1. Start with the core position
   
   Suppose you sell an at-the-money (ATM) straddle at strike 25,250 with 9 days to expiry:
   
   • Short 25,250 CE @ ₹130.9
   • Short 25,250 PE @ ₹126.55

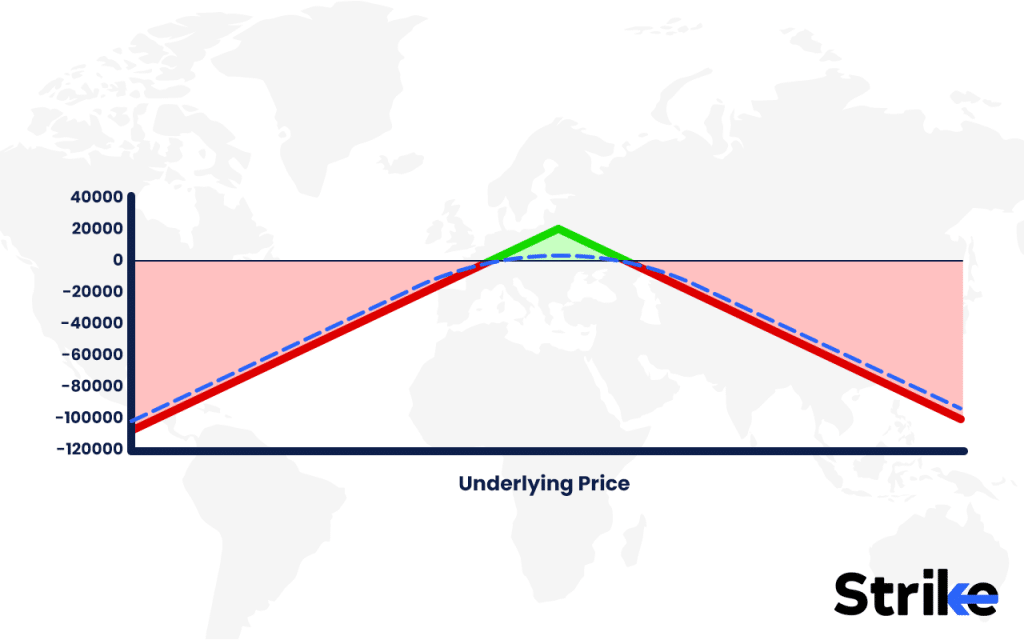
This position is almost delta-neutral (Δ ≈ +0.06) but short gamma (Γ ≈ –0.0025), meaning it loses heavily on sharp price moves but benefits if the price stays near the strike.

2. Add long options to hedge gamma
   
   To reduce the short gamma risk, buy out-of-the-money (OTM) options with good gamma value relative to their premium. Example:
   
   • Buy 25,550 CE @ ₹6.5 (Δ = +0.08, Γ = +0.0013)
   • Buy 25,150 PE @ ₹5.5 (Δ = –0.35, Γ = +0.0012)

This converts the naked straddle into an Iron Fly structure, reducing extreme convexity risk.

3. Check new net Greeks
   
   • Net Gamma = 0.0009 (slightly positive after hedging)
   • Net Delta = 0.08 (remains near neutral)

This adjustment gives more stability and reduces exposure to large price swings.

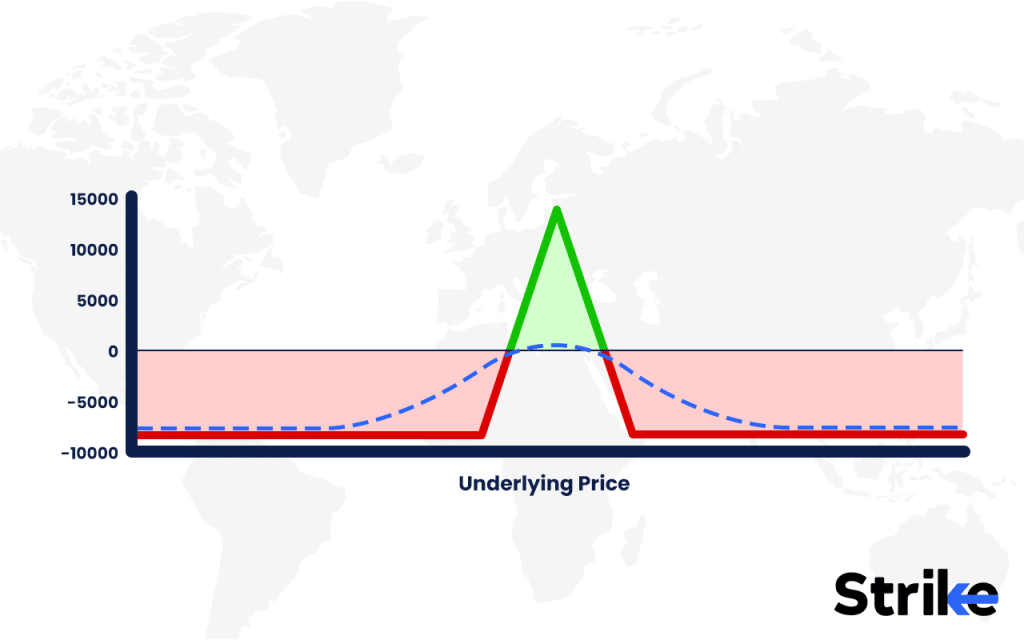
4. Evaluate premium and payoff
   
   • Net Premium = (130.9 + 126.55) – (6.5 + 5.5) = ₹245.45
   • Adjusted Payoff:
     • Max Profit = ₹13,796 (when spot = 25,250 at expiry)
     • Max Loss = ₹8,704 (beyond breakevens)
     • Breakevens = 25,067 (lower) and 25,433 (upper)

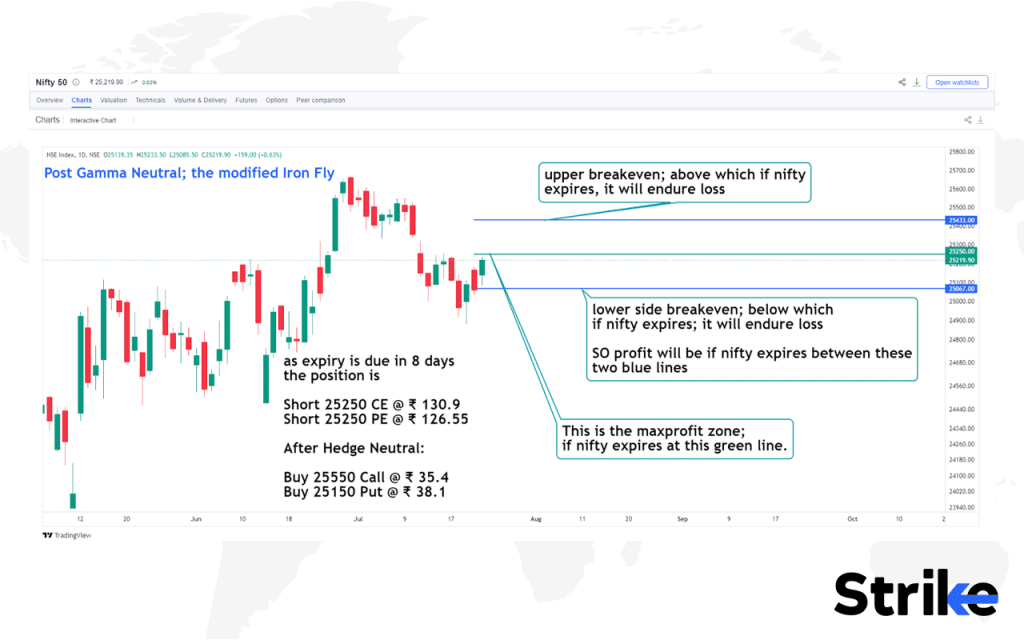
The short straddle, which was initially highly risky with unlimited loss potential, is now gamma-hedged into a controlled payoff structure. While there’s still some residual gamma exposure, the extreme risk is reduced, and losses are capped. This demonstrates practical gamma hedging by converting a naked position into a defined-risk strategy.

What is an Example of a Gamma Hedge?

An example of gamma hedging is managing a short straddle position on Infosys during volatile market conditions. A short straddle has negative gamma, meaning delta changes rapidly against the trader when the stock moves.

Suppose Infosys trades at ₹1,500. A trader sells

• 1 ATM Call (1500CE) at ₹40, Delta = +0.50, Gamma = 0.06
• 1 ATM Put (1500PE) at ₹38, Delta = –0.50, Gamma = 0.06

Initial Net Delta = 0, Net Gamma = –0.12 (short).

If Infosys rises to ₹1,510:

• Call Delta = +0.60, Put Delta = –0.40
• Net Delta = +0.20 (long exposure despite starting neutral)
• Hedge = Short 20 shares (per lot of 100)

If Infosys falls to ₹1,490:

• Call Delta = +0.40, Put Delta = –0.60
• Net Delta = –0.20 (short exposure)
• Hedge = Buy 20 shares

This constant adjustment keeps the portfolio balanced. The trader earns from theta decay on the straddle while offsetting gamma-driven risks. The smoother P/L curve results from hedging delta shifts rather than leaving them unchecked.

What Tools Help in Gamma Hedging?

Gamma hedging requires analytical tools that track Greeks, simulate positions, and suggest rebalancing. Without them, managing real-time exposures is nearly impossible That’s why new age traders use Strike Money.

1. Strike – Offers live option chain, Greeks, strategy builder, and position monitoring. Suitable for both delta and gamma hedging.
2. Sensibull – Provides retail-friendly analytics, including delta, gamma, and payoff charts. Good for event hedging.
3. Quantsapp – Focused on professional traders, gives advanced Greeks analytics and intraday rebalancing recommendations.
4. Bloomberg Terminal / Refinitiv – Institutional-grade platforms offering complete risk analytics and gamma hedging calculators.
5. Broker APIs – Some brokers allow custom-built gamma hedge models through API connections.

Institutions use automated systems that adjust hedges intraday, while retail traders rely on semi-automatic monitoring. The more volatile the environment, the more sophisticated the tool required.

How Option Greeks Affect Gamma Hedging

Gamma is the trigger for delta adjustments, but theta and vega also influence gamma hedging outcomes. Traders must monitor multiple Greeks simultaneously.

• Delta (Δ) – Primary hedge variable. Gamma alters delta as prices shift, requiring rebalancing.
• Gamma (Γ) – Determines the speed of delta drift. Short gamma needs constant hedging; long gamma offers convexity benefits.
• Theta (Θ) – Short gamma positions usually collect theta. Hedging ensures this income is retained while offsetting losses from big moves.
• Vega (ν) – Volatility changes impact option prices. Hedging delta does not eliminate vega risk.

A comparison table

Greek	Impact on Gamma Hedging	Implication
Delta	Needs neutralization	Frequent rebalancing
Gamma	Triggers delta drift	Higher near expiry/ATM
Theta	Offsets hedge costs	Short gamma collects decay
Vega	Adds volatility risk	Unhedged, may swing P/L

Thus, gamma hedging is never isolated—it is multi-dimensional risk control.

How Implied Volatility Impacts Gamma Hedging

High implied volatility increases gamma, leading to more frequent rebalancing and higher hedging costs. Low implied volatility reduces gamma, making hedges more stable.

• High IV Phase – Options are expensive, gamma exposure is higher, and deltas swing aggressively. Hedging costs rise due to constant adjustments.
• Volatility Compression – As IV drops, gamma declines, reducing rebalancing needs. Traders profit more easily from theta decay.
• Volatility-Neutral Portfolios – Advanced traders design positions that balance gamma and vega together, keeping hedges cost-efficient.

Example: Before Infosys earnings, IV spikes to 45%. A short straddle has massive gamma. Traders hedge aggressively. After results, IV falls to 25%. Gamma exposure reduces, allowing fewer hedges and more profit from premium collapse.

What Are the Risks & Costs of Gamma Hedging?

The main risks of gamma hedging include high transaction costs, slippage, and margin usage. While it reduces directional risk, it introduces practical execution challenges.

1. Transaction Costs – Frequent hedges require constant buying and selling of the underlying or futures. Brokerage, taxes, and exchange fees add up.
2. Slippage – Entering hedges at unfavorable prices erodes gains. Fast-moving markets often cause delayed executions.
3. Liquidity Issues – Illiquid underlyings or far-dated options make hedging inefficient.
4. Over-Hedging – Adjusting too frequently may lead to whipsaw losses when markets revert.
5. Market Gaps – Overnight gaps destroy hedges as delta exposure jumps without time to adjust.
6. Margin Requirements – Hedging consumes capital, reducing available liquidity for other trades.

Gamma hedging thus involves a tradeoff: safety vs profitability. Institutions accept higher costs for survival, while retail traders struggle to balance efficiency.

Is Gamma Hedging Profitable?

Yes, gamma hedging is profitable when the cost of rebalancing is lower than the income from theta decay and volatility arbitrage. If costs exceed earnings, the strategy loses money.

• Profit Source: Gamma Scalping – Traders hedge deltas in small oscillations, locking in profits while holding short-gamma positions.
• Loss Source: Hedge Expenses – Too many adjustments eat into theta gains.

For example,

• Short ATM straddle collects ₹50 premium (θ income).
• Gamma hedging costs ₹30 (trading fees + slippage).
• Net Profit = ₹20 per share × lot size.

In volatile markets, gamma scalping often works because frequent swings allow profitable re-hedges. In stable, trending markets, hedging costs outweigh theta income.

Thus, profitability depends on market conditions, execution skill, and cost management.

How to Build a Gamma-Neutral Portfolio

A gamma-neutral portfolio is constructed by balancing option positions and underlying assets so that total gamma exposure equals zero. Traders build it by mixing long and short options at different strikes and maturities.

For example, a trader holding a short ATM straddle has high negative gamma, which makes delta swing aggressively with small price moves. To neutralize, they add long OTM options that carry positive gamma, reducing the convexity risk.

The steps:

1. Compute the gamma of each option position.
2. Multiply by the number of contracts and lot size.
3. Add all exposures to find net gamma.
4. Introduce offsetting trades (often long OTM options) until total gamma ≈ 0.

A gamma-neutral portfolio sacrifices some premium income but reduces violent delta swings. Many institutional desks prefer this method during volatile earnings or event-driven periods.

How Often Should Gamma Be Hedged?

Gamma should be hedged more frequently during high-volatility periods or near expiry. This is because gamma is largest for ATM options close to expiration.

For intraday traders, hedging can be required every hour if the underlying stock is moving sharply. Longer-term traders often rebalance daily, unless markets are calm. The trade-off is between hedge accuracy vs transaction costs.

Automation is common here. Quant desks use algorithms to adjust exposure whenever net delta drifts beyond a threshold (say ±100). Manual traders often rely on broader triggers such as price moves beyond a support or resistance zone.

The key is to accept that over-hedging eats away premium, while under-hedging risks large drawdowns.

What are the Alternatives to Gamma Hedging?

Alternatives to gamma hedging involve using static structures that naturally reduce convexity risk. These methods are cheaper but less precise.

• Vertical spreads – Combining long and short options reduces net gamma without frequent rebalancing.
• Collars – Owning the stock, selling calls, and buying puts caps risk and income.
• Calendar spreads – Selling near-term options and buying longer-term options balances gamma with theta.
• Portfolio diversification – Holding uncorrelated assets instead of dynamically hedging every move.

These alternatives are popular with retail traders who lack the speed or capital for continuous gamma scalping.

What’s the Difference Between Gamma Scalping & Gamma Hedging?

The difference between gamma scalping and gamma hedging is that hedging reduces risk, while scalping seeks profit from volatility. 

Feature	Gamma Hedging	Gamma Scalping
Purpose	Risk reduction	Profit generation
Method	Neutralize gamma to keep delta stable	Trade underlying around hedges to capture volatility
Frequency	Event-based, as needed	Continuous intraday adjustments
Profit driver	Stability, reduced drawdowns	Volatility swings and rebalancing gains
Costs	Transaction + spread	Higher due to constant trading

Both gamma scalping and gamma hedging strategies involve managing gamma exposure but have very different objectives.

What’s the Difference Between Delta Hedging & Gamma Hedging?

The difference between delta hedging and gamma hedging is that delta hedging neutralizes immediate directional risk, while gamma hedging controls how that risk changes with price movement.

Feature	Delta Hedging	Gamma Hedging
Purpose	Neutralize directional exposure (price moves)	Manage changes in delta caused by price movement
Risk Managed	First-order (Δ)	Second-order (Γ)
Method	Offset option delta with underlying/futures	Use additional options to stabilize delta drift
Frequency	Requires rebalancing as delta changes	Requires even more frequent rebalancing during high gamma periods
Users	Market makers, option writers, hedgers	Advanced traders, institutions managing large books
Costs	Lower, due to fewer adjustments	Higher, due to continuous rebalancing and slippage

Delta focuses on first-order risk, whereas gamma deals with second-order sensitivity.