
Delta is a metric that measures the degree and direction an option’s price is expected to move based on changes in the underlying asset’s price. Delta ranges from 0 to 1 for calls and 0 to -1 for puts, indicating the sensitivity of the option’s value to shifts in the spot price. Traders rely on delta for gauging directional outlooks, implementing hedging strategies, structuring spreads, managing volatility trades, and capitalising on asymmetric leverage. However, delta is just an estimate and its nuances around dynamic shifts, gamma flows, time decay, and more should be incorporated into trading decisions.
Understanding delta is crucial for options traders. It provides perspective on the directionality of a position, helping gauge if a trade has bullish or bearish bias. Delta is also key for constructing hedges to offset risks using the negating deltas of put and call options. In addition, delta facilitates creating spreads to finance other legs, targeting specific net exposures. Volatility trading strategies also rely on delta for isolating volatility movements.
Delta is derived using an options pricing model like Black-Scholes. It represents the first derivative of the formula, measuring sensitivity of the option price to changes in the spot. Delta is dynamic, updating constantly as inputs like time decay, implied volatility, and underlying price changes. Time remaining and moneyness also impact delta trends.
Traders utilise delta in many strategic ways. It offers insights into how much an option’s value changes given upside or downside in the underlying asset. Traders also take advantage of delta’s asymmetric properties to magnify percentage returns from small favourable price shifts. However, delta is only an estimate so its nuances must be incorporated into trading decisions.
What is Delta in Options?
Delta measures how much the theoretical price of an option changes in response to a 1-point movement in the price of the underlying asset. Delta is expressed as a number between 0 and 1 which indicates the degree and direction an option’s price is expected to move based on price changes in the underlying.
Delta is calculated by determining the first derivative of the option pricing model, which shows the rate of change in the price of the option relative to changes in the asset price. The most commonly used model is the Black-Scholes model, which takes into account the current asset price, strike price, time to expiration, underlying asset volatility, and risk-free interest rates. Plugging these variables into the model produces the delta value.
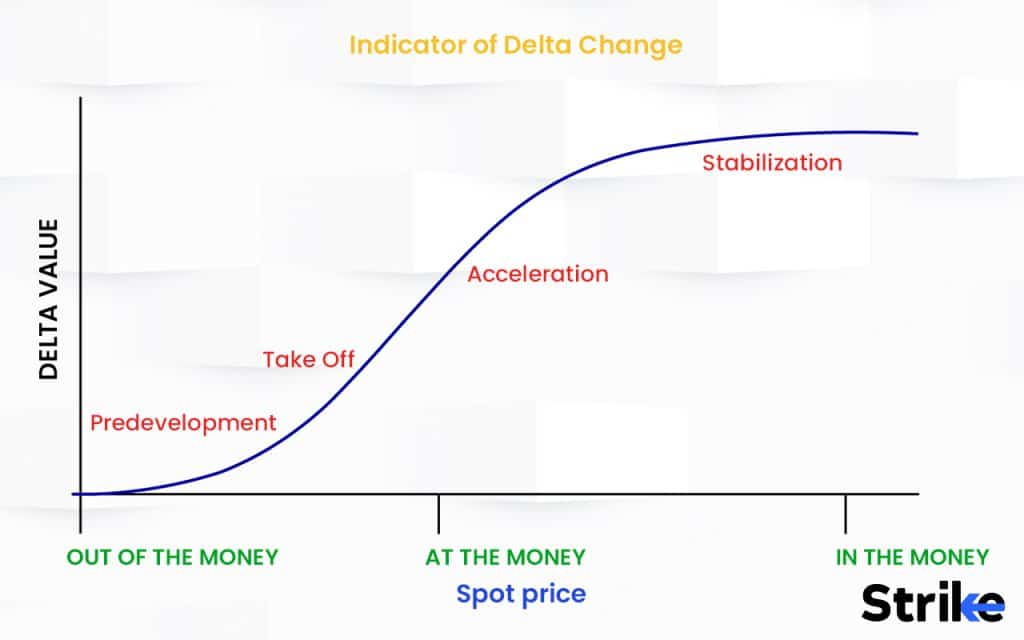
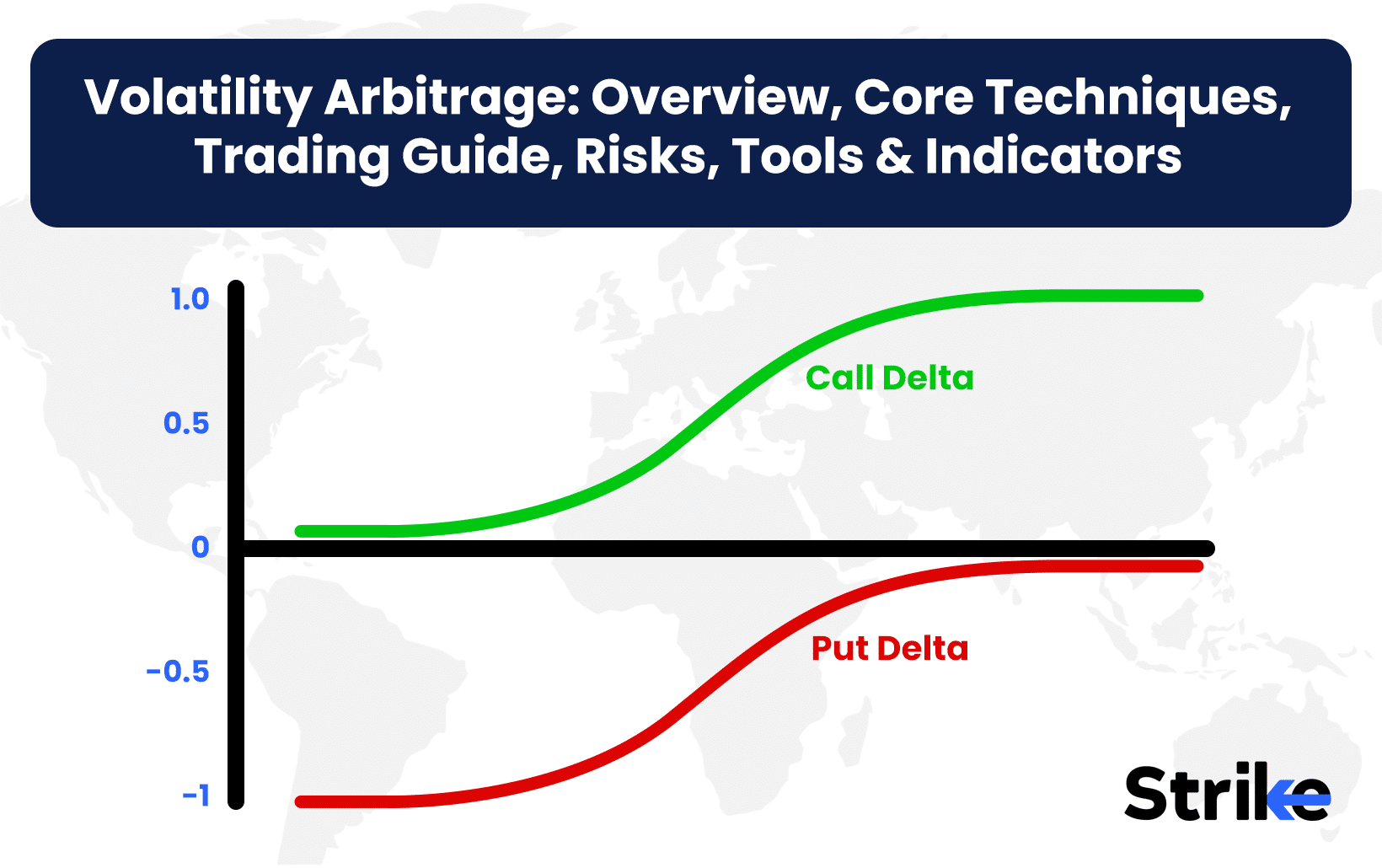
Delta essentially reflects the probability that an option will be in-the-money at expiration. Calls have positive deltas between 0 and 1, indicating the option price will rise as the asset price increases. Puts have negative deltas between 0 and -1, meaning the put price will decline as the asset price rises. At-the-money options generally have a delta of around 0.50 whether calls or puts. Deep-in-the-money options approach a delta of 1.00 as they have a very high probability of finishing in-the-money. Far out-of-the-money options have a delta near zero indicating little price change.
Delta values are constantly changing as the inputs to the option model change over time. As expiration approaches, delta moves toward the extremes of 1 or -1 as the intrinsic value becomes the primary component of the option’s price. Meanwhile, changes in implied volatility of the underlying will also impact delta values. Higher IV results in greater potential price swings, so deltas will be closer to 0.50 at the moment. With lower IV, deltas will gravitate closer to 1.00 for in-the-money and zero for out-of-the-money.
Delta also varies according to the relationship between the asset price and the option strike price. An at-the-money option has a delta of around 0.50, meaning a Rs.1 move in the stock results in a Rs.0.50 move in the option. The option’s delta will increase towards 1.00 if the stock price changes and it becomes more in-the-money. An in-the-money call with a delta of 0.75 implies a Rs.0.75 upside move in the call for a Rs.1 increase in the underlying asset price.
Traders use delta in several strategic ways. First, delta is used to estimate the overall directionality of an options position. The trader who is long 10 calls with a delta of 0.50 creates delta exposure equivalent to being long 500 shares of stock. The total position delta gives a sense of how bullish or bearish the options trade may be. Hedging also relies heavily on delta. Short stock positions are often hedged by buying calls with a delta close to -1 times the number of shares shorted.
Delta hedging involves continually rebalancing the hedge as the delta changes, while gamma hedging accounts for the rate of delta change. Traders construct options spreads around particular delta exposures to benefit from their directional assumptions. For example, bull call spreads involve long lower-delta calls funded by short higher-delta calls to profit from the upside.
The leverage provided by options emerges from delta, as small moves in the underlying translate into substantial percentage gains due to the slope of delta. An at-the-money option only costs Rs.0.50-Rs.1.00 but a 1 point move results in a 50-100% gain. Traders exploit this delta asymmetry through strategies like delta-neutral trading. The position delta is kept close to zero so the trade benefits purely from volatility expansion rather than direction. Delta also impacts options pricing models. The fair value of an option is computed as the discounted expected value of the delta at future points.
While delta is highly useful for assessing the directionality and pricing of options, it does have some limitations. Delta only approximates the expected price change for very small moves. It does not account for gamma, which measures the acceleration in delta. Large price swings violate the assumptions behind delta calculations. Delta also assumes movements are smooth when in reality prices often gap. So the actual option price changed from the delta prediction.
What is the importance of Delta in Options?
The delta of an option is important because it communicates key information about how the option is likely to perform based on moves in the underlying asset. Understanding delta is vital for traders looking to use options effectively for directional bets, hedging, volatility strategies, and more.
Delta is important because it allows traders to estimate the directionality of an option or overall option position. Traders look to delta to gauge how bullish or bearish a particular options trade may be. For instance, a long call position with a delta of +0.70 would generally reflect a bullish outlook. The delta indicates how much the position stands to benefit from an upward move in the underlying asset.
On the flip side, a short put position with a delta of -0.30 would represent a bearish stance, poised to gain as the underlying price declines. By analyzing the aggregate delta of complex options spreads, traders gain perspective on the net directional exposure. Delta provides key insights into how an options trade performs given upside or downside in the underlying asset.
Delta also plays a central role in hedging strategies using options. The delta of an option quantifies how effective it could be in hedging an opposite position. For example, if a trader is short 100 shares of a stock trading at Rs.50, they could neutralize the position by buying a 50-strike call option on the stock with a delta of -0.50. This creates an overall delta-neutral book with minimal directional exposure.
As asset prices fluctuate, traders adjust their options hedge to maintain the desired delta exposure. Delta-hedging aims to hold delta constant as prices change, while gamma-hedging accounts for accelerating delta. Proper delta hedging is crucial for options market makers and institutions offset large directional risks.
In addition, delta informs options pricing models. The fair value of an option is calculated as the discounted expected value of the delta at future points in time. An option’s time value is derived from the probability it will be in-the-money at expiration, which delta represents. Higher delta options have higher intrinsic value, reducing time value. Delta impacts pricing calculations for all types of options, including equity, index, interest rate, currency, and commodity options.
Understanding delta dynamics is vital for trading volatility through strategies like delta-neutral trading. Traders look to profit from volatility itself while remaining delta-neutral. Delta also dictates the unique leverage characteristics of options. Small movements in the underlying asset translate into sizable percentage returns due to delta’s slope.
While delta has some limitations, such as assumptions of smooth and continuous price changes, it remains an indispensable tool for options traders. Delta gives valuable perspective into how sensitive an option’s premium is to changes in the underlying asset price. It quantifies the likelihood an option will finish in-the-money at expiration.
How does Delta in Options work?
Delta works by measuring how much the theoretical value of an option changes in response to a 1-point movement in the underlying asset’s price. Delta indicates the degree and direction an option’s premium is expected to move based on changes in the underlying.
An option’s delta is calculated using a pricing model, most commonly the Black-Scholes model. This model uses variables including the current asset price, strike price, time to expiration, underlying volatility, and interest rates to calculate a theoretical fair value for the option. As part of this calculation, it also produces the delta figure.
The delta output represents the first derivative of the pricing model – in other words, the rate of change in the option’s price relative to changes in the spot price of the underlying. It measures the sensitivity of the option’s value to movements in the underlying asset.
Delta is expressed as a number ranging from 0 to 1 for call options, and 0 to -1 for put options. A call with a delta of 0.50 implies that for a Rs.1 increase in the price of the underlying asset, the theoretical value of the call option will increase by Rs.0.50. The delta of 0.50 represents a 1:1 ratio – changes in the option price in direct proportion to changes in the stock price.
For puts, a delta of -0.30 indicates the put option value is expected to increase by Rs.0.30 if the underlying stock declines by Rs.1.00. The negative delta reflects an inverse correlation between put pricing and the underlying asset price. As the stock price rises, the put becomes less valuable and its delta moves closer to 0.
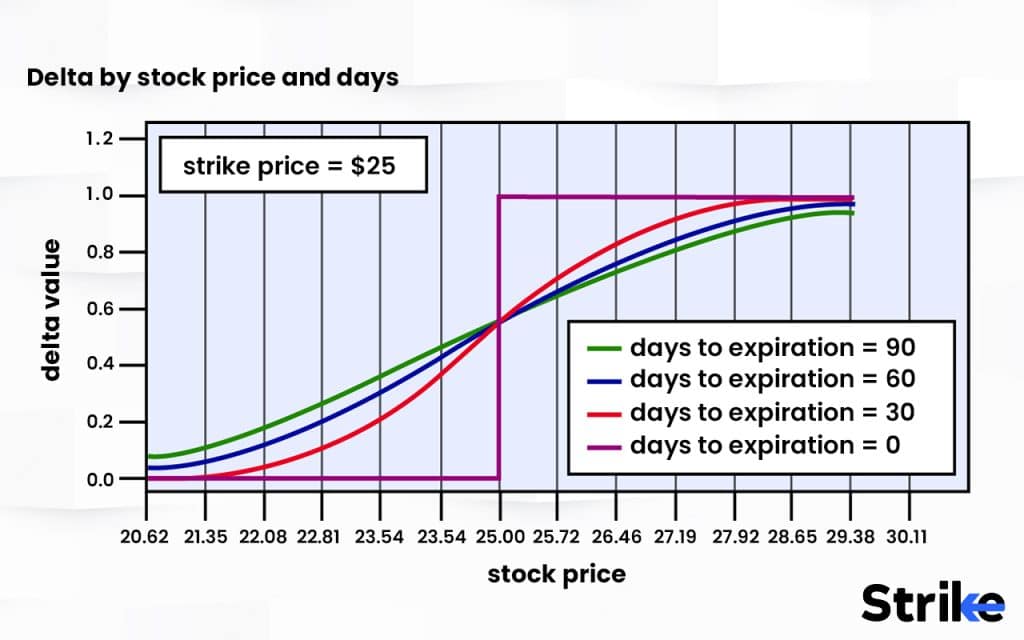
Delta values are constantly updating along with changes in the inputs above. As expiration approaches, an option’s delta will respond more aggressively to price movements in the underlying. Time decay also accelerates delta changes as expiration nears.
Traders monitor delta closely when actively managing an options position. For example, a trader looks to roll an option to a further expiration as it approaches a delta of 1 or -1 in order to maintain the desired exposure.
Delta also tends to change incrementally with each move in the underlying, reflecting the nonlinear returns of options. For a 1-point change, an at-the-money option moves 0.50, but for the next 1-point move, the new delta is 0.52 or 0.48 depending on direction. This nonlinear sensitivity represented by delta underpins many strategic uses of options.
How is Delta calculated in Options?
The Black-Scholes model is used to calculate a theoretical fair value for an option based on multiple variables. These inputs include the current price of the underlying asset, the strike price of the option, time remaining until expiration, estimated volatility of the underlying asset, and risk-free interest rates.
By plugging these parameters into the Black-Scholes formula, it produces an estimated fair value for the option. As part of this calculation, Black-Scholes also outputs the delta of the option.
Delta is derived by determining the first partial derivative of the Black-Scholes formula. In the context of the model, this represents the change in the price of the option relative to a change in the price of the underlying asset. Mathematically, the delta is the first derivative of the pricing function versus the spot price of the underlying.
The delta output is represented in percentage terms, ranging from 0 to 1 for call options and 0 to -1 for put options. For example, a delta of 0.50 indicates that for a Rs.1 increase in the underlying asset’s price, the model estimates the option’s price will rise by Rs.0.50.
While Black-Scholes is the most common method, delta is also extracted using other options pricing models including binomial trees and Monte Carlo simulation.
For a binomial tree model, the delta is derived from calculating the change in option value across each node as the probability of the underlying moving higher or lower changes. Binomial trees map out all possible price paths to expiration in discrete time steps. Delta is measured as the change in option value per price step based on the defined up/down movements.
For Monte Carlo models, thousands of randomly simulated price paths are generated for the underlying asset using defined volatility assumptions. The resulting option value is calculated for each simulation. Delta is then determined by measuring the average change in the option value across all simulations for a given change in asset price.
No matter the pricing model used, the goal is to determine the sensitivity of the option price to changes in the underlying. The model-derived delta provides an estimate of this sensitivity as a ratio of option price movement to a small shift in the underlying.
After initially calculating delta using Black-Scholes or another pricing model, the delta then updates dynamically as the price of the underlying asset fluctuates. Data inputs to the model, including the asset price, implied volatility, and time decay, are constantly changing during market hours.
This means delta must be periodically re-computed using the latest parameter values. Automated calculations ensure delta stays up-to-date as the major inputs evolve, reflecting the most current sensitivity estimate.
How does Delta differ in Put Option and Call Option?
Put and call options on the same underlying asset exhibit differing deltas due to the inverse nature of their price movements. Calls gain value as the underlying price rises, while puts gain value as the underlying price falls. This crucial difference drives the asymmetry in put and call delta values.
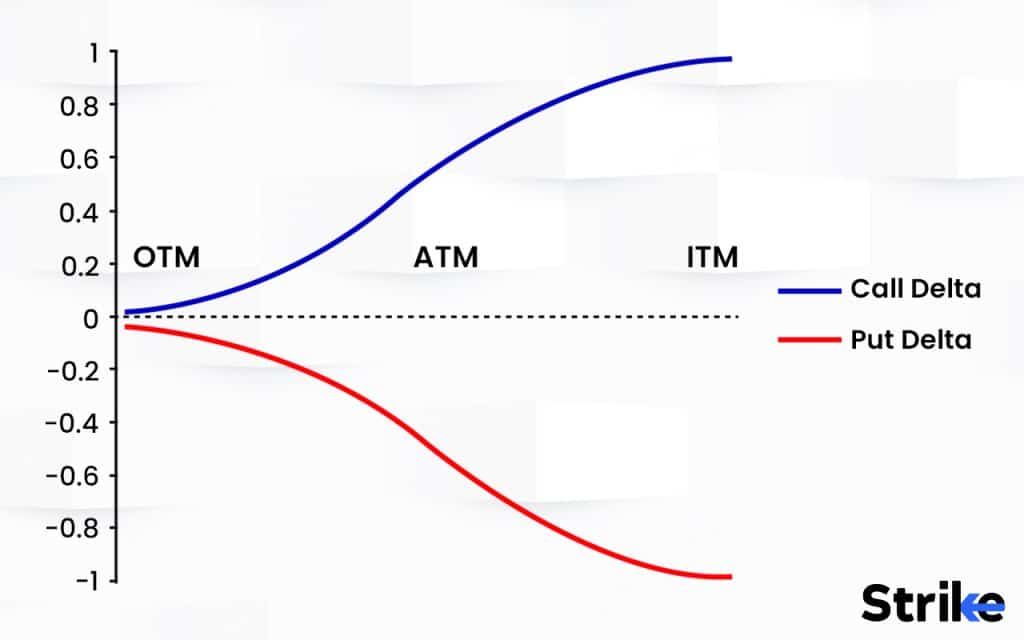
Delta represents the estimated change in option price for a small change in the price of the underlying asset. For both puts and calls, delta ranges from 0 to 1 in absolute value. However, calls have positive deltas, while puts exhibit negative deltas.
A call option has a delta of 0.50, meaning if the underlying rises by Rs.1, the call price is expected to increase by Rs.0.50. A put option on the same asset has a delta of -0.30, meaning if the underlying declines by Rs.1, the put is estimated to gain Rs.0.30 in value.
This delta asymmetry exists because calls and puts have opposing correlations to the underlying asset price. Calls gain value as the underlying increases, reflected in positive deltas. Puts gain value as the underlying declines, reflected in negative deltas.
At-the-money options tend to have similar delta magnitudes close to 0.50 but will be positive for calls and negative for puts. Deep-in-the-money options approach deltas of 1.00 for calls and -1.00 for puts as they mirror the underlying price movements.
Delta also differs across calls and puts due to the effect of time decay. Time decay, or theta, has a negative impact on options prices, gradually eroding the extrinsic time value component. This erosion becomes more rapid closer to expiration.
Since calls have limited downside (the underlying asset only falls to zero), the impact of time decay is more pronounced for puts. As expiration approaches, the delta of in-the-money calls approaches 1 more rapidly than the delta of equally in-the-money puts approaches -1.
Differences in implied volatility between calls and puts also drive delta divergences. Due to leverage provided by calls, market willingness to pay for upside speculation pushes call implied volatility higher than put volatility on the same underlying asset.
Higher implied volatility increases the probability of greater price movement. So the deltas for the high-volatility calls will be closer to 0.50 at-the-money compared to lower-volatility puts. The volatility skew across calls and puts leads to asymmetric deltas.
Moreover, behavioral factors help explain delta differences between calls and puts. A bullish bias is often seen among traders, who think that prices are more likely to rise than fall. This manifests in a greater propensity to purchase calls rather than puts. To keep markets balanced, the heavier demand for calls drives up their prices and deltas relative to puts.
The volatility risk premium also comes into play, as investors are willing to pay more for downside protection from puts compared to leveraged upside from calls. This dynamic also skews put and call deltas in different directions.
How is Delta used in Options Trading?
Traders use delta to gauge potential profit and loss, define risk parameters, and determine optimal positions. The most basic application of delta in options trading is to evaluate the overall directionality of a particular options position. Since delta indicates how much an option’s price changes given a shift in the underlying asset, it signals how bullish or bearish a trade may be.
For example, a long call position with a high positive delta would typically reflect a bullish outlook, while being short a put with a negative delta would represent a bearish stance. Examining net delta across complex multi-leg strategies informs traders on the aggregate directional exposure.
Delta is also vital for options hedging strategies. The purpose of hedging is to neutralise or offset existing risk in a portfolio by taking an opposing position. Delta allows traders to construct options hedges to counterbalance directional risk from any asset type.
A common application is using S&P 500 put options to hedge a long stock portfolio. The negative put deltas offset the implicit bullish delta from being long stocks. Delta-hedging involves continually adjusting the options hedge to maintain a delta-neutral book as prices fluctuate.
In addition, many option spreads are structured around particular delta exposures. For example, a bull call spreads a long lower-delta call option funded by a short higher-delta call. This generates a net positive delta exposing the position to rising prices, while the short call reduces cost.
Conversely, a bear put spread consists of a long high-delta put and a short lower-delta put, creating net negative delta. Delta allows traders to customise spreads for precise directional and risk profiles.
Traders also leverage delta’s asymmetric properties to magnify returns. As an option moves further into the money, small changes in the underlying asset translate into exponentially bigger gains and losses in the option.
Delta neutral trading, in addition, aims to be agnostic to direction by balancing long and short deltas. The goal is to isolate and benefit purely from volatility expansion or contraction. By keeping delta neutral, the trader seeks to earn the volatility risk premium regardless of larger price moves.
What are the factors to consider in using Delta in Options Trading?
The primary factor to consider while using delta in options trading is the fact that Delta is an estimate and not a certainty. Below are eight key considerations that should be kept in mind by traders when adding delta into their options trading selections.
1. Delta is an estimate, not a certainty: Delta provides an approximation of how much an option’s price changes given a small shift in the underlying asset’s price. It does not predict exact price movements. Delta assumes continuous pricing and static conditions, but gaps occur and volatility fluctuates in practice. Traders should view delta as a helpful estimate rather than an absolute certainty.
2. Delta changes dynamically: An option’s delta is not static throughout the life of the trade. As the underlying asset price moves, delta will update accordingly. A 50-delta call option could see its delta rise to 80 if the underlying price increases. Traders must monitor and model potential changes in delta based on anticipated asset price movements.
3. Gamma impacts delta: Gamma represents the rate of change in delta given large movements in the underlying asset. Significant price swings dramatically accelerate or decelerate an option’s delta. Ignoring gamma could lead to delta neutral trades becoming highly directional during big moves. Traders should factor in gamma flows when evaluating delta exposures.
4. Volatility changes impact delt: Delta calculations assume a fixed implied volatility based on the option pricing model inputs. However, in practice IV fluctuates over time, causing deltas to also shift even without price changes. Traders should anticipate how changes in volatility could alter the delta profile of their options positions.
5. Time decay affects delta: As options near expiration, deltas behave very differently due to accelerating time decay. For instance, in-the-money call deltas approach 1 much faster later in the option’s life. Traders should incorporate the potential impacts of time remaining on delta when assessing options.
6. Monitor delta over the trade’s lifespan: The delta profile early in an option’s life looks very different from the delta behaviour closer to expiration. Traders should evaluate how delta evolves and change characteristics across the full lifespan of the options position.
7. Consider delta bleed: Deep in- or out-of-the-money options with deltas near 1 or 0 experiences “delta bleed,” slowly losing sensitivity. Traders should factor in the potential for delta bleed when holding extremely high or low delta options.
8. Balance delta and probabilities: Delta reflects probability of expiring in-the-money, but high delta alone doesn’t guarantee profitability. Traders must weigh delta in the context of other factors like time premiums, break-even points, and potential rate of returns.
While delta is hugely important for options traders, its nuances and limitations should be incorporated into trading decisions. Key factors to consider are delta’s predictive shortcomings, potential for dynamic delta shifts, ignoring gamma effects, volatility impacts, and influence of time decay. Applying delta intelligently while anticipating its complexities enhances options trading outcomes.
What does Delta measure in Options?
Delta measures the degree of change in an option’s price in relation to a change in the price of the underlying asset. Specifically, delta measures the amount an option price is expected to move based on a Rs. 1 change in the underlying asset price.
Delta is considered “moneyness” defined – it indicates how deep in the money or out of the money an option resides at the current underlying price. Higher delta values reflect a greater degree of moneyness for the option.
There are three main reasons why delta correlates to moneyness. Deep-in-the-money options have deltas near 1.0 as they closely mirror the full movement of the underlying with minimal time value. At-the-money options have deltas around 0.50, meaning they move about half as much as the underlying. Deep out-of-the-money options have low deltas near 0.0 as they have minimal sensitivity until major price moves occur.
Delta values draw towards 1.0 or -1.0 as options go deeper into the money with expiration approaching. This shows the option converging to the full risk of the underlying asset or zero as time value decays away.
How to interpret Delta values in Options?
Delta is interpreted using ranges from 0.0 to 1.0 for calls and 0.0 to -1.0 for puts.
At a high level, delta indicates the amount of movement an option price is expected to make based on movement in the underlying. A delta of 0.50 means a Rs. 0.50 move in the option price for a Rs. 1 move in the underlying asset.
Delta also reflects the option’s moneyness – how deep in the money or out of the money it resides. This drives much of the delta interpretation.
Deep-in-the-money options will have deltas near 1.0 for calls and -1.0 for puts. This indicates most of the premium is composed of intrinsic value and the option closely tracks the underlying price.
At-the-money options have deltas around 0.50. Time value comprises about half the premium, so the option only moves around half as much as the underlying asset price. Deep out-of-the-money options have low deltas, often 0.20 or less for calls and -0.20 or less for puts. These have little sensitivity until substantial intrinsic value develops.
Delta is also used as a probability proxy. An option with a 0.25 delta has roughly a 25% chance of expiring in-the-money based on the current underlying price. As expiration approaches, delta for in-the-money options accelerates higher or lower towards 1.0 or -1.0 as time value decays away. Managing this delta convergence is key.
Comparing deltas is helpful for identifying mispriced options. Look for unusual deltas relative to an option’s moneyness or other options at similar strikes and expiration dates. In strategizing trades, balance delta versus other factors like time value and strike distance. Lower delta options have lower probability but higher potential rewards if successful.
Monitor overall portfolio delta across multiple option positions to manage net directional exposure. Delta hedging involves trading the underlying to offset option delta risk.
What is a good Delta for Options?
The ‘good’ delta of a particular delta depends on the trader’s strategy, market outlook, and risk management preferences. There are, nevertheless, specific criteria for delta values.
For speculative trades looking to profit from large upside or downside swings, traders often target options with deltas closer to 0. These out-of-the-money options offer high leverage, and amplified returns from a big move in the underlying price. However, the delta is low, so they have a higher chance of expiring worthless if the anticipated price swing does not materialize.
For conservative trades seeking to hedge or generate income, traders prefer higher delta options. An at-the-money call with a 0.50 delta or greater provides greater protection against adverse underlying moves. The higher delta also indicates larger premiums to potentially collect. However, the cost to enter these options is higher too.
A delta-neutral strategy, when constructing spreads, aims to make the position insensitive to underlying price action. This involves combining long and short options to create an overall delta near zero. For example, selling a 0.50 delta call and buying a 0.50 delta put would create a delta-neutral spread.
For covered calls, traders want sufficient upside exposure, so they select deltas around 0.30. This allows some stock price appreciation while benefiting from call premium decay. Very high call deltas above 0.70 defeats the purpose of a covered call strategy.
Portfolio managers use delta to determine the appropriate hedge ratio when hedging equity exposure with index options. The delta informs the quantity of puts or calls needed to offset the portfolio sensitivity. Higher delta options require fewer contracts to hedge.
What does 25% Delta mean in Options?
A 25% delta means the option is expected to move Rs.0.25 for every Rs.1 move in the price of the underlying asset. This indicates relatively low price exposure.
The delta of an option measures the estimated change in the option’s price relative to a 1-point change in the price of the underlying asset. It is expressed on a scale from 0 to 1.0, representing the expected price movement as a percentage of the underlying price shift.
A call option with a delta of 0.25 indicates the option price is projected to increase by 25 cents if the underlying stock price rises by Rs.1.00. The 0.25 delta tells us the option only has about one-quarter of the price exposure of the underlying.
Similarly, a put option with a delta of -0.25 suggests the put price will rise by 25 cents if the underlying stock declines by Rs.1.00. Again, the option price is moving just a fraction compared to the underlying.
Options with deltas around 0.25, whether calls or puts, are considered relatively insensitive to small changes in the stock price. They are likely out-of-the-money to some degree. Their price tends to experience little change from mild fluctuations in the underlying asset.
However, as options with deltas of 0.25 transition further out-of-the-money or into-the-money, their price and delta become more responsive. The delta approaches 0 when deep out-of-the-money. The delta moves closer to 1.0 when deep in-the-money.
A 0.25 delta option must experience a substantial move in the stock price before its own price and profitability are impacted in a major way. Traders know there is risk of losing the entire premium paid if the anticipated price move does not materialize prior to expiration.
What does 0.5 Delta mean in Options?
A 0.5 delta means the option is expected to move Rs.0.50 for every Rs.1 move in the underlying asset price. This indicates moderate exposure and sensitivity.
A call option with a 0.5 delta suggests its price is projected to rise by 50 cents if the underlying stock price increases by Rs.1.00. The 0.5 delta conveys moderate price exposure – a 50% sensitivity relative to upside moves in the stock.
Similarly, a put option with a delta of -0.5 indicates the put price is estimated to gain 50 cents if the stock declines by Rs.1.00. Again, a moderate inverse price exposure is present.
Options trading with a delta of 0.5 are considered at-the-money. This means their strike price aligns closely with the current trading price of the underlying asset. At-the-money options exhibit the highest sensitivity – even small movements in the underlying rapidly impact the option’s price and delta.
Traders understand a 0.5 delta option will experience accelerated gains/losses compared to the stock if it transitions into-the-money. As it moves further in-the-money, the delta approaches 1.0. The delta declines toward 0 when it falls out-of-the-money.
The moderate sensitivity of a 0.5 delta option provides a balance of leverage and intrinsic value. There is less risk of losing the entire amount paid compared to lower delta options. But the cost is also higher than lower delta options allowing less leveraged return.
Is high Delta good for Options?
Yes, high delta options are advantageous for conservative traders looking to hedge an existing portfolio or generate income. A high delta (delta closer to 1.0) means the option price will track the underlying asset price very closely. A high delta call acts almost like owning the stock. The drawbacks are high delta options have a higher upfront cost. And the trader cannot benefit from dramatic price swings in the underlying. Essentially, high deltas exchange leverage for the probability of profit.
Does Delta increase closer to expiration?
Yes, the delta tends to increase as an option gets closer to expiration. The reason the delta increases near expiration is because there is less time value remaining. Time value decreases as expiration gets closer, so intrinsic value becomes a larger component of the option’s price.
Since delta measures sensitivity to the underlying asset price, which is intrinsic value, it increases as extrinsic time value decays over time.
What are the advantages of Delta in Options?
Risk assessment is the key advantage of using Delta in option trading. Below are the main six advantages.
Risk Assessment
Delta indicates the sensitivity of the option’s price to changes in the underlying asset price. Higher absolute deltas mean greater risk exposure. This helps traders evaluate the risk-reward profile of a potential options trade. Lower deltas have less risk but less premium value.
Hedging
Delta is useful for determining hedge ratios – the number of option contracts needed to hedge an existing portfolio. For example, considering you own a Rs.100,000 stock portfolio, buying 10 S&P 500 put options with a -0.50 delta could provide an effective hedge.
Market Outlook
Delta helps traders select options suitable for their market outlook. Bullish outlooks favour calls with higher positive deltas. Bearish outlooks favour puts with higher negative deltas. Targeting the right delta gives traders options exposure that aligns with their projected price movements.
Liquidity Insights
Options with very high or very low deltas tend to have wider bid/ask spreads due to lower liquidity. Options with mid-range deltas around 0.50 tend to have the tightest spreads and greatest liquidity.
Strategy Suitability
Delta gives insights into which options strategies may be appropriate. For example, covered calls favour deltas around 0.30, while delta neutral trades target a delta of zero. Comparing the delta values of different option strike prices helps determine the best strategy fit.
Greeks Interactions
Delta also provides clues into how the other Greeks like gamma, theta, and vega change at different underlying price points or time periods. Understanding delta dynamics improves Greek analysis.
Delta is a versatile options trading metric that allows informed risk management, alignment with market forecasts, cost-efficient trading, strategy selection, and Greek analysis. Delta provides substantial advantages when used properly.
How accurate is Delta in Options?
Delta is reasonably accurate for estimating the expected price change of an option given a small change in the underlying asset price. However, delta does have some limitations in its accuracy.
Delta is most accurate for small price changes in the underlying. The approximation assumes a linear relationship between the option price and the underlying price. However, in reality, this relationship is nonlinear.
Delta accuracy starts to break down with larger price swings. This is because delta does not account for gamma, which represents the acceleration in delta given bigger moves in the underlying.
Additionally, delta only considers changes in the underlying price, not other factors like time decay or volatility shifts, which also affect the options premium. So while directionally accurate, the expected magnitude of price change may be over or underestimated.
Delta is also not constant – it changes as the underlying price moves and time passes. Traders have to continually monitor and update delta to keep it relevant. The accuracy of static delta quotes deteriorates quickly.
Delta accuracy also depends on general market conditions. In calm, range-bound markets, delta tends to be more predictive. But in very volatile markets, large unexpected price swings cause delta to be less reliable.
How much Delta is suitable for option selling?
Selling options with very low deltas is suitable when expecting limited underlying movement. A delta around 0.10-0.20 provides high theta decay with minimal directional exposure. However, premium income is also lower.
Selling options at-the-money with deltas around 0.50 offers greater premium income potential. But short sellers need to actively manage the position as delta exposure is higher. Hedging is recommended to offset directional risk.
In low volatility environments, selling options with higher deltas around 0.70-0.80 capture greater premiums while keeping risk reasonable. The key is maintaining flexibility to adjust the strikes sold as volatility fluctuates.
During periods of elevated volatility, keeping delta exposure very low becomes critical. Avoid selling options with deltas above 0.30, as short positions quickly become threatened by adverse underlying moves.
Rolling to different strikes or expirations allows option sellers to maintain appropriate deltas. For example, they need to roll out-of-the-money as the market rises to keep delta exposure around 0.30.
Is a 0.3 Delta good for selling?
Yes, a 0.3 delta is generally a suitable level for option-selling strategies. Selling options with a delta around 0.30 offer a good balance of premium income versus directional risk exposure. Option sellers aim to profit from the decay of time value as options near expiration. They want to sell options with sufficient premium to generate income, but minimal exposure to underlying price movements.
A delta of 0.3 implies moderate sensitivity to the underlying asset price. The option only moves about 30 cents for every Rs.1 move in the stock. This delta level provides some cushion against market fluctuations impacting the sold option.
At the same time, a 0.3 delta option will have more time value priced into the option premium than lower delta choices. This offers greater income potential to the option seller.
A 0.3 delta option is considered out-of-the-money, so the seller is not capping significant upside potential. The underlying still appreciates before becoming threatened.
The moderate 0.3 delta exposure is stable in most market conditions. But if volatility rises sharply, the option seller needs to buy back the contract or roll to a lower delta option to stay profitable.
Are there disadvantages of Delta in Options?
Yes, there have been certain drawbacks or limits to using delta for options trading that traders should be aware of. Delta is valuable for gauging the sensitivity of an option’s price to movements in the underlying asset. However, delta does have some drawbacks traders need to consider.
Delta only approximates sensitivity for small price changes. The relationship between the underlying price and option premium is nonlinear, so the delta becomes less accurate for larger moves. Delta does not account for other factors like time decay and volatility that also impact option prices.
So the expected price change from delta alone may be over or underestimated. Delta is not constant – it changes as market conditions change. Traders must continually update and monitor delta to keep it relevant, which takes time and effort.
In very volatile markets, delta lose reliability as large, unexpected price swings cause greater inaccuracy in the projected price movements. Delta values are theoretical estimates. Realised option price changes differ significantly from what deltas had signaled, especially for illiquid options.
What are examples of Delta in Options?
Here are five examples of how delta works in options trading.
Call Option with 0.25 Delta
A call option on stock XYZ has a delta of 0.25.
This means if XYZ rises Rs.1, the call option is expected to increase by Rs.0.25.
Since the delta is relatively low, the option only moves 1/4 as much as the stock.
Put Option with -0.60 Delta
A put option on index ABC has a delta of -0.60.
The put is expected to gain Rs.0.60 in value if ABC declines by Rs.1.
The negative delta indicates an inverse relation to the underlying index.
At-the-Money Call with 0.52 Delta
A call option on stock QRS has a current delta of 0.52.
The delta is right around 0.50 indicating the option is at-the-money.
The call option will gain about Rs.0.52 if QRS rises Rs.1.
The call option will lose about Rs.0.52 if QRS declines Rs.1.
Deep In-the-Money Call with 0.98 Delta
A call option on commodity GHI has a high delta of 0.98.
Being deep ITM, its price behaves almost identically to the underlying.
The call is expected to increase to Rs.0.98 if GHI rises Rs.1.
The very high delta indicates strong sensitivity.
Delta-Neutral Spread at 0.00 Delta
A trader constructs a spread by selling a 50 delta call and buying a 50 delta put.
This creates a position with a net delta of zero.
The delta-neutral spread means there is minimal exposure to the underlying asset.
Small price movements in either direction have a limited impact on the spread.
Can Option Delta be 1?
Yes, an option’s delta can be 1 under certain circumstances. An option’s delta measures the rate of change in the option’s price relative to a change in the price of the underlying asset. Delta ranges from 0 to 1 for calls and 0 to -1 for puts. A delta of 1 indicates a 1:1 relationship between the option price and the underlying price.
This occurs when the option is deep in-the-money. For example, consider a call option with a strike price of Rs.50 on a stock trading at Rs.100. Since the option is Rs.50 in-the-money, if the stock price increases by Rs.1, the call option price will increase by Rs.1 as well. The option behaves almost exactly like owning the stock outright. Therefore, the delta would be close to 1.
As expiration approaches, an in-the-money call option’s delta approaches 1 and an in-the-money put option’s delta approaches -1. At expiration, the delta on an in-the-money option will be exactly 1 or -1. This is because there is a certainty the option will expire in-the-money, so its price moves dollar-for-dollar with the stock price.
Can Options Writing use Delta?
Yes, option writers use delta to help manage their positions and risk exposure. Here is an explanation of how delta applies to options writing: Delta is very important for options writers because it indicates how much their option position will change in value with a move in the underlying asset. Understanding delta allows writers to hedge their options and balance their overall portfolio deltas.
Option writers will dynamically hedge their deltas as prices change. The trader would short more shares to get back to a delta-neutral position if the call delta increases to 0.60. This adjustment of deltas through trading the underlying is how writers mitigate directional risk.
In addition, traders choose to write options at specific delta levels to express a directional view. For example, selling out-of-the-money puts with a delta of 0.20 expresses a bullish outlook. The writer sees upside potential but wants downside protection if they are wrong. Delta allows precision in expressing market opinions.
What is the difference between Delta and Gamma in Options?
Delta and gamma are related but differ because they measure different sensitivities in how the option price changes.
Delta measures the rate of change in an option’s price relative to a change in the underlying asset’s price. Delta ranges from 0 to 1 for calls and 0 to -1 for puts. Delta approximates the probability an option will expire in-the-money. Delta is the first derivative of the option pricing model.
Gamma measures the rate of change in an option’s delta relative to moves in the underlying price. Gamma indicates how quickly delta changes as the stock price moves. Gamma is highest when the option is at-the-money. Gamma is the second derivative of the option pricing model.
Delta is a linear approximation, gamma is nonlinear.
Delta is higher when an option is in-the-money, and gamma is highest at-the-money.
Delta ranges from 0 to 1, gamma is often 0.01 to 0.05.
Delta helps hedge directional risk, gamma helps hedge convexity risk.
An option’s delta is mostly affected by time to expiration and moneyness, gamma is mostly affected by volatility.
For traders, delta implies how many shares are needed to hedge while gamma implies how often the hedge needs adjustment. Managing both Greeks is crucial for options market makers and hedgers.

![85 Common Stock Market Terminologies for Dummies [Updated List for 2026] 52 85 Common Stock Market Terminologies for Dummies [Updated List for 2025]](https://www.strike.money/wp-content/uploads/2025/04/Popular-Stock-Market-Terms-for-Beginners-Banner.png)







No Comments Yet.