A Volga option is an exotic type of option contract that derives its value from realized volatility of the underlying asset rather than just the price of the asset. The Volga option allows traders to isolate and capitalize on volatility while remaining delta-neutral to price movements. Volga options offer leveraged exposure to volatility spikes and enable unique trading strategies. The name Volga refers to the winding Volga River in Russia, analogous to how volatility shifts unpredictably.
Volga options are structured to pay out based on the magnitude of change in the realized volatility of the underlying asset. The payout is proportional to the difference between current realized volatility and a strike volatility specified in the option. Traders isolate and leverage volatility exposure while eliminating directional risks. The key parameters are volatility strike, observation period, and payout ratio per percentage volatility.
The biggest advantage of Volga is that it provide leveraged exposure to volatility spikes and enables capitalizing on periods of high volatility. Volgas often have lower liquidity and wider bid-ask spreads compared to standardized options, which is the biggest limitation.
What is Volga in Options?
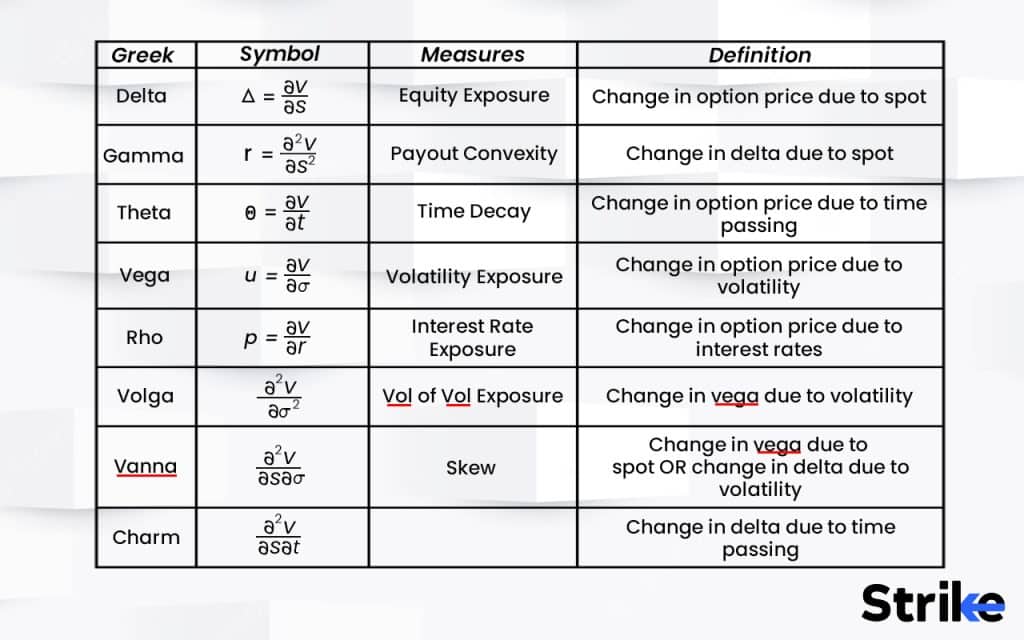
Volga, also known as volatility gamma, is a second-order option Greek that measures the rate of change in an option’s vega with respect to changes in the underlying asset’s volatility. Volga indicates how much vega itself changes in response to volatility fluctuations, just as delta measures the sensitivity of an option’s price to changes in the underlying asset price and vega measures sensitivity to volatility,
Mathematically, it is expressed as Volga = δ2V/δσ2
Where V is the option value, σ is the volatility, and δ2V/δσ2 is the second partial derivative of V with respect to σ.
Volga indicates the rate at which an option’s vega changes as volatility changes. Vega changes rapidly with volatility if Volga is high. Vega remains relatively steady despite volatility shifts if Volga is low.
Volga is a quadratic Greek, meaning it involves the second derivative of the option price. Other quadratic Greeks include Vanna (rate of change of delta with respect to volatility) and Vomma (rate of change of vega with respect to the underlying price).
Volga measures the sensitivity of vega to changes in volatility. Vega itself measures the sensitivity of an option’s price to volatility. So while vega quantifies how much an option’s value changes with volatility shifts, volga indicates how much vega changes with the same volatility shifts.
For example, an option could have a vega of Rs. 100. This means the option price is expected to increase by Rs. 100 if volatility rises by 1%. Vega will rise by Rs. 150 if volatility rises by 1% if the Volga for this option is Rs. 150.
So in this example, a 1% volatility increase would raise option value by Rs. 100 initially. But due to the high Volga, Vega would then rise by Rs. 150, making the option even more sensitive to further volatility changes.
Volga is often referred to as “vega convexity” because it reflects the nonlinear, convex relationship between vega and volatility. As volatility rises, vega increases in a curved, accelerating manner rather than a straight line. Volga quantifies this curvature.
Volga is closely related to vomma, though they measure different sensitivities. Vomma represents the first derivative of vega with respect to changes in the underlying asset price. It indicates how much an option’s vega changes based on movements in the underlying price.
Volga represents the second derivative of option price with respect to volatility. It measures how much vega itself changes when volatility changes.
So Vomma focuses on underlying price changes, while Volga focuses purely on volatility changes. However, they both provide information on how vega behaves.
Vomma and Volga also tend to trend in the same direction. Options with high Vomma tend to also have high volga. Their values are linked because vega depends on both underlying price and volatility.
Why is Volga significant in Options Trading?
Volga is significant in options trading because it lets traders profit from volatility changes independently of the underlying asset’s price moves, enabling pure volatility trading strategies.
Volga measures how much an option’s vega changes in response to a 1% change in volatility. Without Volga, it is impossible to know exactly how much Vega exposure will change when volatility shifts. Volga provides this critical missing piece of information.
Volga also informs traders about how rapidly vega exposure changes when volatility moves. A higher Volga means vega changes dramatically even with small volatility fluctuations. Lower Volga means vega remains more stable despite volatility changes.
This speed of vega changes is crucial for risk management. Vega hedging modifications must be done quickly to adapt to new volatility levels if Volga is high. Knowing Volga allows properly anticipating the pace of vega exposure changes.
Another reason Volga is so important is because Vega does not change linearly with volatility. Instead, the relationship is convex, vega increases at an accelerating rate as volatility rises. Volga encapsulates this nonlinearity. The convexity of vega means Volga increases alongside rising volatility. This reflects the accelerating sensitivity. Without modeling the Volga, it is impossible to accurately capture Vega’s convex behavior. Volga is the only way to quantify this crucial nonlinear relationship.
How does Volga differ from other option Greeks?
Volga differs from other option Greeks because it belongs to a special category of second-order option Greeks. Most Greeks like delta, gamma, and theta are first-order derivatives, volga is a second-order derivative measuring the rate of change of vega relative to volatility.
This unique nature means Volga provides a distinct perspective on option sensitivities. Below we will explore how volga differs from primary Greeks like delta, gamma, theta, and vega itself.
Delta measures the rate of change of option price relative to movements in the underlying asset price. It quantifies price sensitivity to the underlying. Volga measures the rate of change of vega with respect to volatility. It quantifies the sensitivity of vega to volatility shifts.
While delta gauges direct price exposure, Volga examines the sensitivity of volatility exposure. Delta looks at primary impact, Volga looks at secondary impacts.
Gamma is the rate of change of delta relative to underlying price moves. It indicates how rapidly delta changes as the underlying asset price fluctuates.
Volga parallels gamma in that it measures the rate of change of a first-order Greek. But volga measures changes in vega rather than delta, and relates to volatility rather than underlying price.
So while gamma looks at changing delta sensitivity, Volga examines changing vega sensitivity at different volatility levels. Both are second-order Greeks looking at the convexity of primary Greeks.
Theta measures the rate of change of option price relative to time decay as expiry approaches. It quantifies sensitivity to passage of time. Volga relates to changes in vega sensitivity to volatility, not passage of time. Theta and Volga measure entirely different option price sensitivities.
Theta gauges chronological sensitivity, while volga examines sensitivity to volatility shifts independent of time.
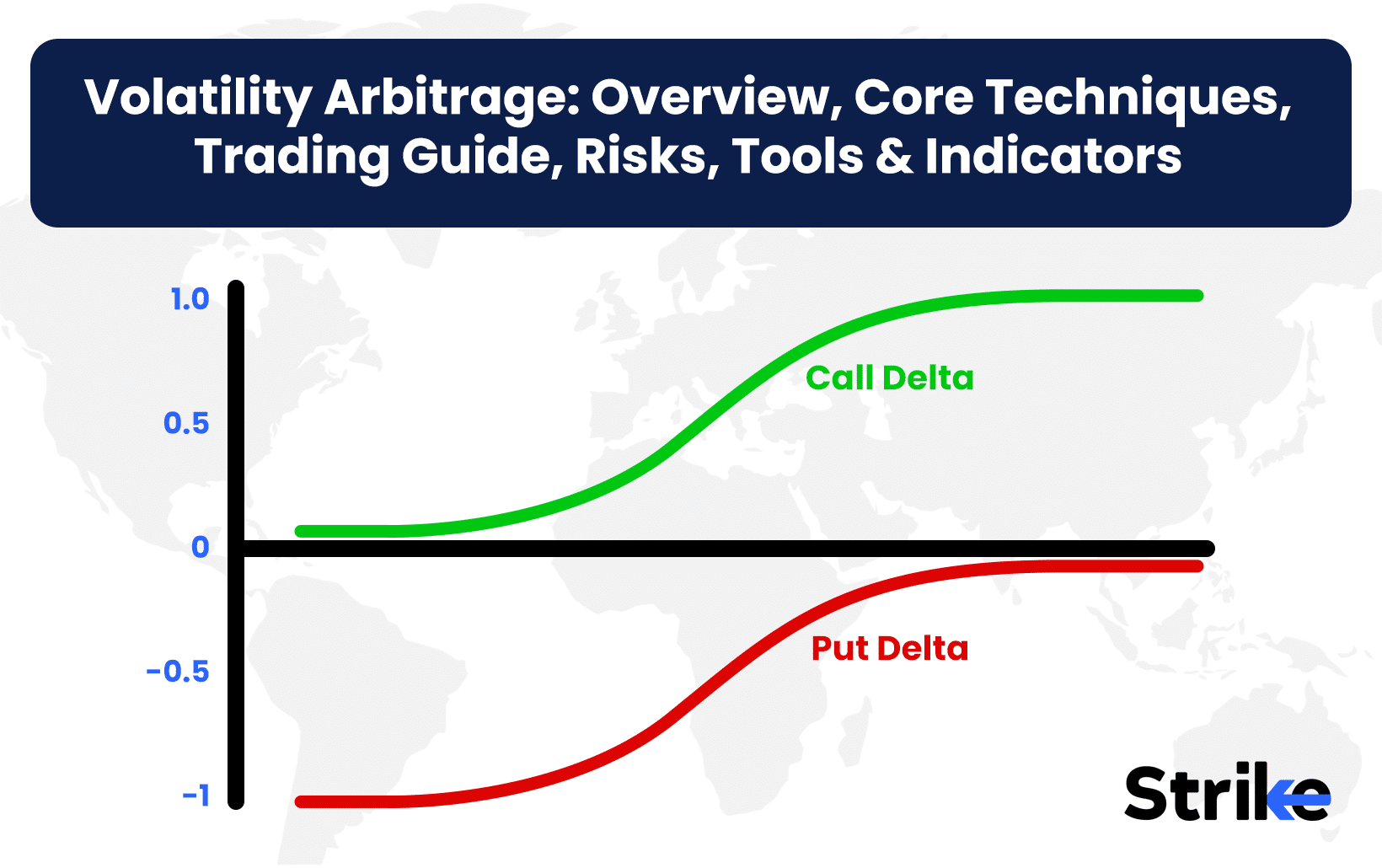
Vega measures the sensitivity of option price to changes in implied volatility of the underlying asset. It quantifies exposure to volatility.
Volga examines the rate of change of vega relative to movements in volatility. It measures the second-order exposure to volatility. So vega quantifies primary volatility sensitivity, and volga examines the rate of change of that primary vega sensitivity at different volatility levels.
What is the relationship between Volga and Vega options?
The most direct relationship between Volga and Vega is that Volga represents the first derivative of Vega with respect to volatility. It quantifies the rate at which vega changes in response to a shift in volatility.
While vega is linear, Volga exposes the nonlinear, convex relationship between vega and volatility. As volatility increases, vega does not change in a straight line. Rather, it accelerates higher in a convex curve. For instance, vega increased by 0.5 for a volatility rise from 20% to 21%. But from 30% to 31%, vega increased by 0.8. This acceleration is quantified by Volga. It reflects the second-order sensitivity and asymmetric response of vega to volatility shifts.
Traders use both Volga and Vega together to fully understand an option’s volatility exposure. Relying solely on vega provides an incomplete picture. Vega shows the current absolute exposure, while Volga indicates how rapidly that exposure will change. Evaluating them jointly provides critical insights for risk management. For example, an option has high vega but low Volga. This means volatility risk is currently large but relatively stable. Conversely, low Vega but very high Volga indicates muted risk presently but exposure could quickly accelerate if volatility rises.
Another key relationship is that options with elevated vega tend to also have proportionally high Volga. Out-of-the-money options exhibit the highest vega since they gain sensitivity as the underlying price approaches the strike. These OTM options also see their vega change dramatically with volatility fluctuations. So the high vega corresponds to sizable Volga as well due to the sensitivity.
Sophisticated options traders implement strategies that target disparities between Vega and Volga across different contracts. For example, they look to sell expensive volatility by shorting high vega/Volga options and buying lower vega/Volga options as a hedge. Traders also trade Volga directly when it is rich or cheap relative to theoretical values. This allows benefiting from Volga converging toward its fair value.
Options hedgers utilise Volga to offset the convexity of Vega that exacerbates risk. Due to its innate convexity, vega increases nonlinearly as volatility rises. This makes volatility risk difficult to hedge dynamically. Analysing Volga allows properly sizing hedge adjustments to counteract the accelerating vega. This minimises volatility risk, even during market crashes and spikes.
How does Volga work?
Volga works by providing options payouts based on the magnitude of change in realized volatility rather than just the price of the underlying asset. The key parameters in a Volga option are the volatility strike, observation period, and payout ratio. The volatility strike is the level of volatility chosen as the reference point for the payout structure. The observation period is the timeframe over which realized volatility is tracked. The payout ratio determines how much the option pays out per percentage point of volatility difference.
Traders buy Volga calls when they expect volatility to rise and Volga puts when they expect it to fall. The payouts scale proportionally to the magnitude of volatility change in either direction. By eliminating exposure to the underlying price, Volga provides pure exposure to realized volatility changes. If volatility increases more than the strike, Volga call options pay off based on the percentage difference even if the price is flat.
The realized volatility is computed from the standard deviation of daily log returns over the observation window. Proprietary pricing models use advanced techniques to value Volga options based on factors like implied volatility, skew, interest rates, etc. Volga enables isolating strategies to trade volatility spikes while avoiding risks from directional price swings. Traders customize parameters like observation period and payout ratios to match their volatility forecasts and risk appetite.
What is the formula for calculating Volga?
The following formula is used to determine an option’s Volga.
Volga = Change in Vega / Change in Implied Volatility
Or expressed mathematically as
Volga = dVega / dVolatility
For example, say an option has:
Vega = 0.10
Implied Volatility = 20%
The Volga would be the following if implied volatility rose by 1%, causing Vega to climb to 0.105:
Volga = (New Vega – Original Vega) / (Change in Volatility)
Volga = (0.105 – 0.10) / (21% – 20%)
Volga = 0.005 / 1%
Volga = 0.5%
Therefore, this option has a Volga of 0.5%. This means vega increases by approximately 0.5% when implied volatility rises by 1%.
Typically Volga is quoted in percentage terms rather than absolute value. This represents the proportional change in vega relative to the change in volatility.
The Volga formula is derived from the mathematical relationship between vega and implied volatility.
Vega measures the first partial derivative of option price with respect to volatility:
Vega = δValue/δVolatility
Volga measures the second partial derivative:
Volga = δVega/δVolatility
Which is equivalent to:
Volga = δ2Value/δVolatility2
Taking the partial derivative of vega with respect to volatility gives us the formula for calculating Volga.
The Volga formula provides the proportional change in vega relative to a percentage change in volatility. The Volga ratio isolates the relationship between Vega and volatility independently of the option price. This conveys the acceleration in vega as volatility changes.
How does Volga contribute to the sensitivity of options to changes in implied volatility?
Volga plays a key role in determining how sensitive an option’s price is to shifts in implied volatility levels by quantifying the rate of change in vega. This indicates how rapidly an option’s exposure to volatility fluctuations shifts. Here is an in-depth look at the mechanisms through which Volga contributes to implied volatility sensitivity.
The primary way Volga impacts volatility sensitivity is by expressing the nonlinear, convex relationship between Vega and volatility. As implied volatility rises, vega does not increase linearly. Instead, it responds at an accelerating rate that curves upward. This convexity means small changes in volatility trigger large vega sensitivity shifts when Volga is high.
For example, a 1% increase in volatility from 20% to 21% boosts vega by 0.5. But the same 1% volatility increase from 30% to 31% could increase vega by 0.8 due to the convexity. Volga provides the exact quantification of this effect, showing how much more rapidly Vega reacts at higher volatility levels. This convex dynamic directly contributes to amplified volatility sensitivity.
In addition to the convex relationship, Volga also expresses the sheer rate of change of vega with respect to volatility. Mathematically, Volga represents the first derivative of vega relative to volatility. This measures the marginal effect on vega from a volatility shift.
The higher the Volga value, the larger the resulting adjustment to Vega from even tiny volatility moves. Volga essentially provides a multiplier effect on vega as volatility changes. For example, an option with a Volga of 50 would see its Vega increase by Rs. 50 for every 1% rise in implied volatility. The high Volga translates to large vega sensitivity shifts.
The magnitude of Volga determines how significantly it impacts overall volatility exposure. The higher the Volga number, the greater its influence on vega sensitivity. The low Volga means volatility shifts only slightly adjust vega, limiting changes in exposure. But very elevated Volga creates massive vega sensitivity changes from small volatility movements. This explains why deep out-of-the-money options exhibit the greatest volatility sensitivity. Their higher vega and Volga act as dual accelerants on volatility exposure.
Due to its effects on vega sensitivity, Volga also amplifies the P&L outcomes of volatility trading strategies. Volatility exposure becomes more pronounced when Volga is high. This means any upside or downside volatility moves will result in larger P&L swings.
Strategies such as long straddles, short strangles, and long vega greatly benefit from expansive Volga, as it compounds profits from favourable volatility shifts. Managing Volga is key for volatility traders.
How does Volga impact options and their pricing dynamics?
Volga impacts options pricing and valuation by quantifying the sensitivity of vega to changes in implied volatility. Through its influence on vega, Volga directly affects how option prices respond to volatility shifts. The higher the Volga, the more dramatic the price changes from volatility fluctuations.
Volga effectively acts as an accelerant on options prices, magnifying the implications of volatility movements. Small fluctuations in volatility cause big price swings when the Volga is high since the Vega exposure is shifting quickly.
This dynamic stems from the Volga encapsulating the convexity between vega and volatility. As volatility increases, vega responds at an accelerating, nonlinear rate. Volga provides the exact measure of this acceleration.
For example, a 1% volatility increase boosts Vega by 0.5 when Volga is 50. But if Volga is 100, that same volatility increase could spike Vega by 1.0 or more. This translates to larger price moves.
The end result is that Volga amplifies the overall price sensitivity to volatility. Options with elevated Volga see their values fluctuate wildly with even modest volatility shifts. Managing the Volga is key for risk management.
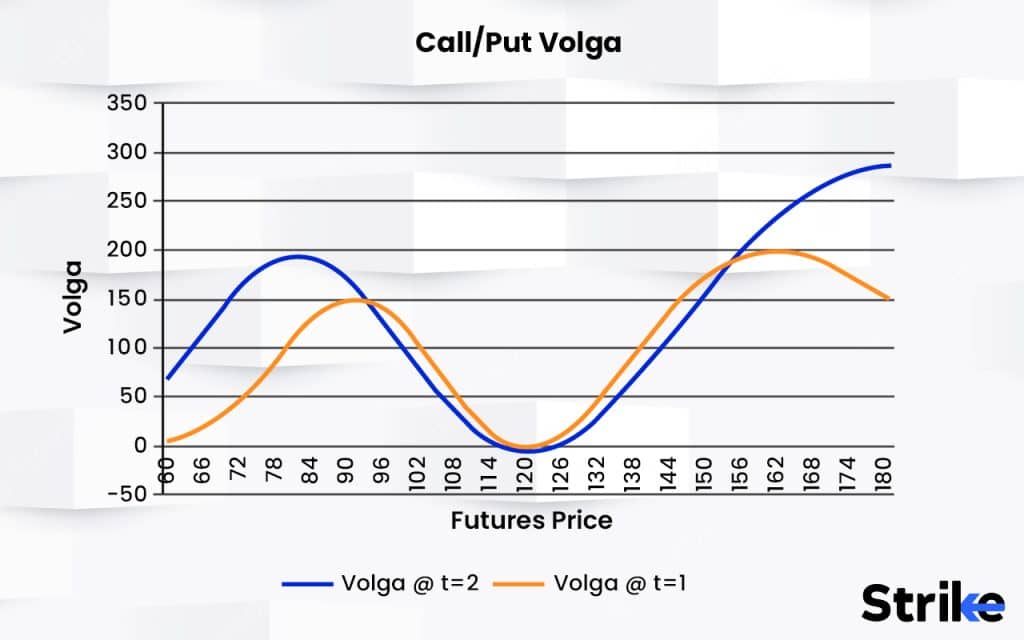
Volga also differs significantly across options based on moneyness and time to maturity, further contributing to pricing inconsistencies.
At-the-money options exhibit the highest Volga values, which explains their oversized price reactions to volatility changes. Out-of-the-money options have very low Volga.
Additionally, short-dated options experience a dramatic Volga increase near expiration. This leads to exaggerated price volatility compared to longer-dated options.
Traders utilise these Volga nuances to structure positions optimally for volatility trading strategies. The moneyness and expiration with the highest Volga provide maximum exposure to volatility swings.
Volga also holds importance in the options pricing models used to derive fair value. The Black-Scholes model relies on multiple volatility assumptions. Since Volga quantifies vega’s response to volatility, it is a key input used to price options dependent on implied volatility. Volga must be accurately incorporated to capture the nonlinear vega effects.
Pricing complex options with stochastic volatility requires meticulous Volga calculations. As volatility dynamics grow more complex, so does the significance of Volga in valuation.
What strategies can traders employ to handle Volga risks?
Trading Volga options offers significant opportunities to capitalize on volatility movements but also introduces risks that require prudent management. Below are ten strategies traders employ to handle Volga risks.
Hedge Other Greeks
Since Volga only conveys vega risk, hedging other Greeks is key. Using spreads or complementary options to hedge delta, gamma, rho and theta exposure ensures volatility moves do not create outsized losses. Hedging non-volatility risks curtails the impact of extreme Volga changes.
Incorporate Directional Views
Rather than purely volatility-focused, trades should incorporate directional views on the underlying. This provides greater flexibility to adjust positions should volatility move adversely. Combining directional and volatility perspectives offers more latitude.
Favour Longer Expirations
Longer-dated options have lower Volga, so their Vega is less sensitive to volatility shifts. Focusing on longer expirations when possible provides more stable exposure even when targeting high Volga contracts. The slower vega decay also helps sustain positions.
Actively Manage Time Value Decay
As options age, the declining time value deflates Volga and Vega. Making timely rolls or adjustments avoids having volatile exposure decrease right when it is needed most. Offsetting time decay enables maintaining higher Volga targets.
Hedge Vega Convexity
Volga expresses Vegas’ nonlinear convexity that accentuates risk. Hedging tools like futures, variance swaps, and CBOE S&P 500 Volatility Index (VIX) options help offset convexity risks by rising when volatility spikes occur.
Trade Volga Differentials
Instead of outright volatility directional bets, trading the difference between theoretical vs. actual Volga isolates profitable volatility discrepancies. This spreads the impact of whipsaws if volatility reversals occur.
Utilise Spread Strategies
Call or put spreads lower costs while defining risk parameters. Vertical spreads, butterflies, condors, and other structured trades allow benefiting from Volga divergences while limiting extreme volatility impacts.
Diversify Across Strikes
Volga varies significantly by strike, peaking for at-the-money options. Constructing positions across multiple strikes helps balance exposure and smooth out volatility sensitivity. Strike diversification curbs Volga risk concentrations.
Leg Into Positions
Building positions over time when entering trades allows reassessing along the way as new volatility data emerges. This mitigates excessive commitment at once, providing flexibility to adjust sizing as risks evolve.
Maintain Prudent Leverage
While Volga trading necessitates leverage to amplify gains, restraint is critical so that accessible leverage does not exceed risk limits. Having modest buffer room on credit lines avoids margin calls or liquidations when volatility spikes.
By incorporating these risk-aware tactics, traders pursue Volga-based strategies while implementing protections against extreme vega fluctuations or adverse Greek exposures. The optimal approach utilises Volga to maximise volatility opportunities while managing associated risks.
What factors influence Volga in option trading?
The key factors that affect the scale of Volga in options trading are Strike Price, Time to Expiration, Implied Volatility, Interest Rates, and Skew. Below is an explanation of each.
Strike Price
Volga is highest for at-the-money options and declines as you move further in-the-money or out-of-the-money.
Time to Expiration
Volga declines as expiration approaches due to time decay. Longer-dated options have higher Volga.
Implied Volatility
Volga increases when implied volatility rises and decreases when IV falls. Vega and Volga have a proportional relationship.
Interest Rates
Volga decreases when interest rates rise, as the discount factor in pricing models reduces. Lower rates increase Volga.
Skew
Volga is amplified when the skew is greater as volatility smiles widen. A higher skew exposes options to larger volatility moves.
Traders actively evaluate these factors to determine optimal entry points when targeting Volga exposure. Managing these drivers is key to effectively trading Volga-based strategies.
How does Volga behave under different market scenarios?
Volga sometimes behave differently under different market scenarios. In periods of rising implied volatility, Volga will increase across the entire options surface. As overall volatility levels rise, the vega exposure of all options becomes more sensitive. This translates to higher Volga values.
Traders capitalise on increasing Volga in a rising volatility regime by buying options with the highest baseline Volga, since their exposure will accelerate the most. Selling expensive volatility by shorting high Volga options also grows more profitable as their Vega risk builds.
All options experience a decrease in Volga when implied volatility is steadily declining. With lower volatility levels, options have lower overall vega and less sensitivity to further volatility changes.
To benefit from declining Volga in a compression volatility regime, traders sell expensive options that still maintain elevated Volga. As their Volga decreases, these shorts become less exposed to volatility rebounds.
In strong trending markets, Volga differences between various strikes become more pronounced. At-the-money options see their Volga spike higher as they gain volatility sensitivity at the fulcrum of the trend. Out-of-the-money options see Volga decline as they move farther from the money.
Traders capitalise on these divergences by selling expensive ATM volatility while buying cheaper OTMs options to benefit if the trend continues or reverses. Focusing on strike divergences is key.
Volatility and Volga variations across strikes are minimal when the underlying is range-restricted. Without a directional trend, no strikes stand out as having greater sensitivity. This flattens out the Volga curve across moneyness.
In these scenarios, directly trading Volga is less advantageous than capitalising on directional range breaks. Volga trading thrives on volatility divergences rather than subdued environments.
In the event of a sudden, sharp move in the underlying, Volga spikes dramatically across all options in the direction of the breakout. This reflects rapidly increased vega exposure from the outsized price swing.
Traders vulnerable to volatility should hedge or reduce positions ahead of potential binary events that could trigger sharp moves. The resulting Volga spike acts as an accelerant on volatility exposure requiring risk reduction.
Analysing how Volga evolves in different market conditions provides insights into appropriate trading strategies and risk management. Adapting to shifting volatility and moneyness divergences allows capitalising on Volga trading opportunities as they emerge.
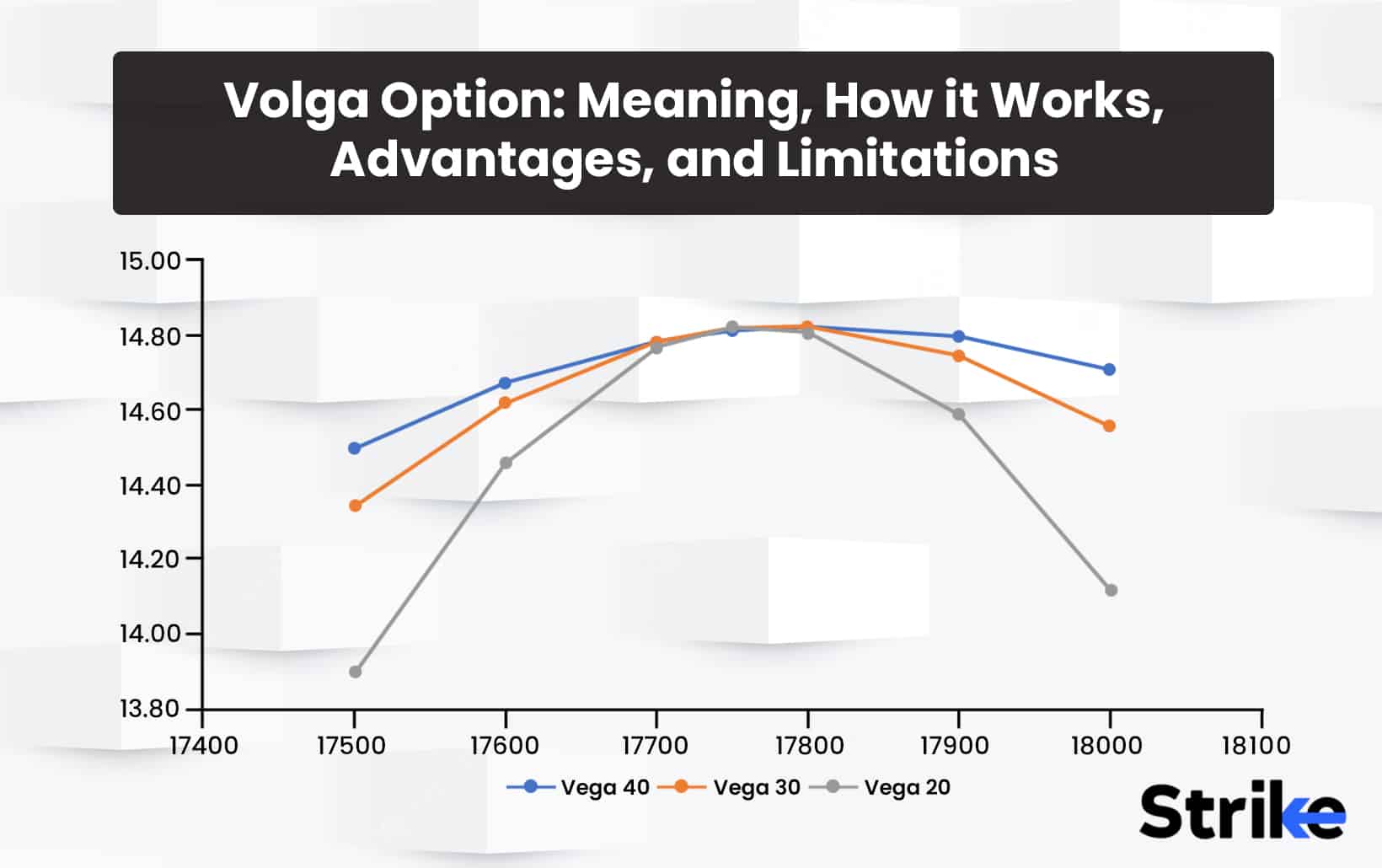
How does Volga behave for at-the-money options versus in-the-money or out-of-the-money options?
At-the-money (ATM) options, with the underlying price near the strike price, exhibit the highest Volga values. Maximum vega sensitivity occurs for options straddling the money. This peak Volga for ATM options occurs because small underlying price movements quickly shift options in or out of the money. This dynamic vega exposure contributes to elevated Volga. Traders tend to favour using ATM options when constructing trades expressly for Volga exposure. The higher sensitivity produces the greatest reaction to volatility changes.
In-the-money (ITM) options have declining Volga as they move further into the money. Deep ITM options have very low Volga levels. This occurs because ITM options behave more akin to the underlying asset itself, with less sensitivity to volatility fluctuations. Their premium consists more of intrinsic rather than time value.
ITM options still retain modestly higher Volga compared to equally out-of-the-money options on the other side of the underlying price. This effect is more pronounced for puts than calls.
Far out-of-the-money (OTM) options have very low Volga, but it increases gradually as the strike nears the money. This uptrend continues until Volga peaks for ATM options. While OTM options have greater vega in absolute terms, their vega is less sensitive to changes in volatility. Their already limited probability of expiring ITM reduces Volga effects.
Deep OTM options see their Volga decline steadily as they move farther from the money and any realistic probability of profit. They act more like leveraged directional bets.
What strategies can be employed when trading Volga options?
Long volga, short volga, volga spreads etc. are the most commonly employed strategies when trading volga options. Below is a detailed explanation.
Long Volga
Buying options with high Volga provides greater upside exposure if implied volatility rises. Traders target elevated Volga options to maximise sensitivity to expected volatility increases.
Short Volga
Selling expensive volatility through options with high Volga results in profit if implied volatility declines. The short benefits from the high vega options losing extrinsic value.
Volga Spreads
This involves buying low Volga options while selling high Volga options of the same underlying. Profit comes from the two Volga exposures converging over time.
Strikes Spreads
Traders go long ATM options with highest Volga while shorting cheap OTM options to fund the trade. Benefits if volatility expands or contracts.
Calendar Spreads
Going long near-term high Volga options and shorting lower Volga longer-dated options capitalises on the Volga term structure.
Diagonal Spreads
Combining differences in both Volga and expiration dates allows profiting from relative Volga opportunities.
Straddles/Strangles
Utilising high Volga ATM straddles or OTM strangles gains exposure to sharp volatility moves in either direction.
Volga Scaling
Constructing positions with differential Volga across multiple options creates asymmetry in the volatility exposure.
Time Spreads
Selling near-term elevated Volga options to fund buying longer-term high Volga options that have less time decay.
Combos/Synthetics
Pairing options with equity or futures contracts allows crafting unique risk profiles with Volga exposures.
VIX Options
Incorporating VIX options provides direct exposure to index volatility while also trading the Volga differences.
As a sensitivity indicator, Volga allows creatively managing volatility exposure across varied strikes, expirations and underlyings. Traders utilise Volga options in tailored combinations to generate income, hedge risks, or capitalise on volatility opportunities.
What are the benefits of trading Volga options?
Investing in options with a concentration on the Volga will provide the nine main advantages. This includes magnified volatility exposure, insights into vega exposure etc.
Magnified Volatility Exposure
High Volga options greatly amplify exposure to implied volatility changes. Even small volatility moves result in outsized gains if directionally positioned correctly.
Hedge Vega Risk
Volga provides insights into current vega exposure and future changes in vega. This allows intelligently managing volatility risk through informed hedging.
Take Advantage of Volatility Skew
Differences in Volga across strikes allows capitalising on volatility skew. Traders isolate the most overpriced or underpriced volatility points.
Volatility Mean Reversion
High Volga options are sensitive to volatility reversals back to the mean. Strategies target reversion from extremes.
Leveraged Returns
The use of options provides leveraged exposure to maximise returns from accurate volatility forecasts and modelling. Margin requirements on options allow enhancing profitable Volga trades.
Defined Risk
Unlike volatility products like VIX futures, options strategies allow defining maximum loss parameters through spreads or position sizing.
Lower Correlation
Volatility trading through options provides returns less correlated to equity and bond markets. This diversification benefits portfolios.
Trade Volatility Directly
While risky, trading Volga enables benefiting purely from volatility swings as a distinct asset class rather than indirectly through other assets.
Cost Efficiency
Options provide volatility exposure more efficiently than alternatives like futures contracts or swaps which have higher margin costs.
Volga-focused option trading provides magnified volatility exposure, improved risk management, diversification, and strategic opportunities unavailable through purely directional options approaches. Volga unlocks unique volatility-based strategies and return sources.
How do Volga options provide potential opportunities for traders to capitalise on changes in implied volatility?
Volga options give investors the potential opportunity to profit on changes in implied volatility in a number of significant ways. Options with high Volga exponentially increase in value when implied volatility rises, and decrease more dramatically when volatility declines. This magnified exposure allows traders to capture larger gains from accurate volatility forecasts.
Even small changes in implied volatility result in major returns if the appropriately high Volga options are held. The convexity makes the options almost like a volatility-based leverage vehicle when directionally positioned correctly.
The tendency for elevated volatility to eventually decline back towards historical norms creates mean reversion trading opportunities.
Options with inflated Volga due to a volatility spike are expected to experience falling Volga as the volatility normalisation occurs. Strategies designed to capture this mean reversion effect generates consistent income.
Traders sell expensive volatility by shorting high Volga options, expecting the positions to benefit as Volga decreases when exaggerated volatility declines. The mean reversion makes high Volga shorts statistically profitable over time.
Volga frequently varies significantly across different option strikes, even for the same underlying and expiration. This volatility skew enables Volga arbitrage strategies.
Traders sell ATM volatility while buying cheaper upside/downside out-of-the-money volatility with lower Volga to capitalise on the divergence if there is a particular inflation of Volga for at-the-money options due to demand.
Isolating mispriced volatility across the skew allows crafting spreads that benefit from Volga converging and skew normalisation. The complexity of Volga creates frequent short-term skew mispricings to target.
Options inherently have greater sensitivity to volatility rises then declines due to convexity. This makes hedging volatility risk challenging.
Analysing Volga enables properly sizing hedges to counterbalance the asymmetric convexity risk. Volga provides the inputs needed to hedge vega exposure that changes dramatically when volatility spikes or plunges occur.
Volga-based options trading provides amplified volatility exposure, capitalises on mean reversion tendencies, targets temporary skew mispricings, and manages convexity risks. Volga’s complexity creates volatility-based opportunities.
What are the limitations of trading Volga options?
Model risk, liquidity constrains, and Vega decay are the main limitations of trading Volga options. Below are the main ten limitations listed.
Model Risk
Volga relies on options pricing models that require assumptions subject to errors. Incorrect Volga estimation undermines trading strategies reliant on accurate theoretical values.
Liquidity Constraints
Thin markets for some contracts, strikes, or expirations make executing Volga trades difficult at optimal prices. Wide bid-ask spreads also constrain potential profits.
Vega Decay
Even high Volga options experience declining vega over time. This vega decay erodes Volga, undercutting longer-term trades.
Unhedged Risk Factors
A purely Volga-driven focus ignores other Greeks that affect risks. Losses emerge from unhedged exposures like delta, gamma, and rho.
Volatility Reversals
Strategies betting on a Volga increase from rising volatility face sudden losses if volatility spikes then swiftly mean-reverts lower. Predicting future realised volatility is challenging.
Complacency Risk
Prolonged low volatility regimes lead to cheap hedging costs. This complacency makes traders vulnerable to unpreparedness for eventual volatility expansion.
Complex Greeks Interactions
It is difficult to fully isolate Volga from other shifting Greeks in real trading. Unintended exposures emerge subtly over time.
Costs and Frictions
Frequent rebalancing required in Volga trading involves transaction costs that erode profits. There are also margin and borrowing costs on leverage required.
Uncertain Long-Term Studies
Academic research on Volga trading efficacy over long periods is relatively limited compared to other Greek-based strategies.
Event Risk
Binary events like earnings or economic data suddenly spike implied volatility and Volga before positions are hedged, creating significant losses.
While an insightful volatility indicator, real-world trading based on theoretical Volga has model risk, decay challenges, liquidity constraints, and risks from unhedged factors and market surprises. An adaptive, measured approach to Volga trading is prudent.
Are there any specific market conditions or events that can significantly impact Volga?
Yes, specific market circumstances and developments have a big influence on Volga for options. Quarterly earnings announcements frequently generate sharp overnight implied volatility spikes and drops as information is released. This rapid volatility shift causes substantial changes in Volga across all strikes.
Major economic data releases like jobs reports or GDP causes swift volatility reactions as traders digest the news. The new information changes expectations, impacting Volga.
Statements or speeches from Federal Reserve officials often dramatically alter interest rate policy expectations. This impacts volatility across asset classes, influencing Volga, especially for rates-sensitive sectors.
Sudden geopolitical developments like war, sanctions, or elections quickly increase uncertainty, driving sharp but fleeting volatility spikes. The rapid shifts affect Volga.
The new or withdrawn equities experience spiking volatility as a result of increased trading activity when the index membership is rebalanced. Their options’ Volga increases.
Implied volatility increases as a result of the costly hedging as borrow rates soar for companies that are widely shorted. Any associated options exhibit heightened Volga.
Takeover announcements cause a spike in M&A target share volatility. The associated options see short-term inflated implied volatility and Volga.
A big company’s bonds and stock volatility increase if it receives a credit downgrading due to projected default risks. Related options have surging Volga.
What is the expected return on a Volga option?
There is no singular expected return inherently associated with Volga options. Options dependent on the Volga might make money or lose money depending on a number of variables.
Much like other options strategies, the directional outlook for future realised volatility is a key driver of potential returns. A long Volga option investment makes money if volatility increases. But if volatility declines, the position loses money.
The magnitude of the change in implied volatility also determines the gains or losses. Larger changes in volatility equate to greater Volga-driven returns, whether positive or negative. Small changes drive small returns.
Since Volga is a theoretical calculation, the accuracy of the Volga value affects strategy returns. Volatility risk and rewards are lower if Volga is undervalued. Overestimated Volga overstates potential profits.
Over longer holding periods, the effects of vega decay erode Volga, reducing exposure the longer the options are held. Expected returns rely on precisely anticipating holding periods.
Options with longer time to maturity have greater cumulative volatility exposure. Near-term options see Volga decay rapidly lower as expiration nears, undercutting potential returns.
Transactions costs, funding costs for leverage, and bid/ask spreads all lower net realised gains from Volga option positions. Returns must exceed these frictional costs.
Proper hedging of non-Volga risks like delta exposure improves isolating profitable Volga-driven returns. Unhedged risks contribute to losses or gains separate from Volga.
The scale of Volga option trades also impacts gains. Larger size means greater dollar profits from favourable volatility moves. Smaller size reduces both upside returns and downside risk.
How does the expected return on a Volga option vary based on different market conditions and implied volatility levels?
The implied volatility regimes and various market situations have a significant impact on the projected return on Volga options. During prolonged periods of low volatility, the expected return on long Volga options decreases. With subdued volatility, there is less potential upside even for high Volga options. Expected returns rely on a volatility expansion kickstarting Volga exposure.
The anticipated return on long Volga options rises when implied volatility is high. More potential exists for further volatility spikes, generating gains for long Volga positions. Short Volga expected returns also improve as volatility means reverts lower.
Expected gains on Volga holdings depend on whether implied volatility is considerably skewed across strikes and whether the skew will normalise or continue to be severe. Traders must accurately forecast skew behaviour, not just volatility direction.
Ahead of known volatility events like earnings, expected returns relying on Volga increase as traders anticipate expansion. But this priced-in volatility also raises costs, lowering expected returns from overpriced options.
After an event catalyses a volatility spike, expected returns for short Volga positions increase. Volga is elevated but likely to decrease as volatility stabilises, benefiting shorts.
In bull market regimes, upside Volga call options see higher expected returns. Puts have lower expected gains if volatility rises during an upward trend as the puts fall more out-of-the-money.
The complexity of Volga means contextual analysis is required. Changing market conditions alter the factors influencing Volga-driven expected returns for any given strategy. Adaptive trading approaches are optimal when isolating profitable Volga opportunities.
What are some common misconceptions associated with Volga?
The idea that higher Volga means better trade is one of the most common misconceptions associated with Volga. Below is a list of eight common myths related to Volga.
Higher Volga Means Better Trades
False. Simply pursuing the highest possible Volga options does not guarantee better results. Potential gains come with higher risks if volatility moves adversely. Intelligent strike and expiration selection are crucial.
Volga Alone Captures All Volatility Risks
Incorrect. While a key volatility Greek, Volga does not encompass all vega-related risks. Traders must also assess baseline vega, gamma, theta, and other Greeks holistically to mitigate risk.
Volga Signals Future Volatility Direction
Misleading. Volga only measures the sensitivity of vega to volatility changes. By itself, Volga provides no actionable information on whether future realised volatility will be higher or lower.
Volga is Always Accurately Predictable
Not true. While theoretical Volga can be calculated, myriad factors cause real-world deviations. Expecting observed Volga to align consistently with models is unrealistic. Approximations suffice for trading.
Higher Volga Means Higher Vega
Sometimes false. Options with elevated Volga tend to also have high vega, but not always proportionally. Scenarios occur where vega is substantial but Volga remains muted and stable despite volatility shifts.
Volga is More Important Than Delta
Misguided. While a key volatility Greek, focusing solely on Volga ignores directional risks. Traders incur major losses from adverse delta exposure despite favourable Volga positioning.
Volga Trading Has No Risk
Incorrect. Volga trading carries significant risks, including unanticipated volatility direction, skew changes, early exercise on American options, and unhedged Greeks. No trading is riskless.
Volga Behaves Similarly Across Asset Classes
Not necessarily accurate. While directionally similar, nuances in Volga arise across equities, forex, rates, and commodities due to differences in structure. Unique inputs and behaviours affect Volga.
While Volga enables insightful volatility analysis, real-world trading success relies on realistic assumptions accounting for risks, volatility unknowns, Greek interactions, pricing deviations, and model shortcomings. An adaptive, measured Volga approach is optimal.








No Comments Yet.