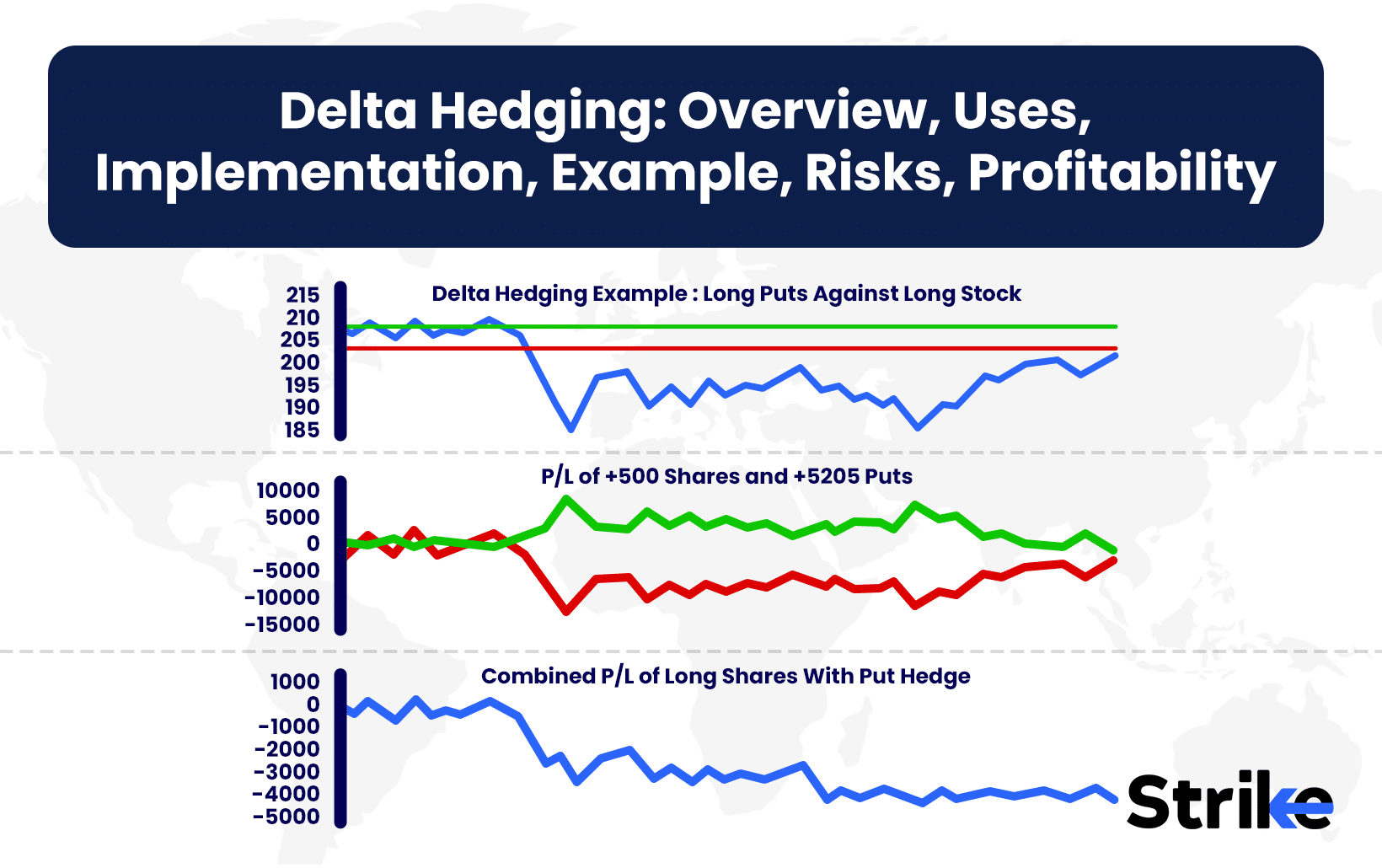
Delta Hedging: Overview, Uses, Implementation, Example, Risks, Profitability

Delta hedging is a strategy that reduces an option or portfolio’s directional risk by offsetting delta exposure with positions in the underlying asset. Delta hedging is used to maintain a delta-neutral stance, ensuring that small price moves in the stock do not significantly impact the overall profit or loss.

The key idea is that options are sensitive to stock price changes through their delta. By balancing this delta exposure, traders control directional bias and instead focus on earning from time decay or volatility. Institutions, hedge funds, and market makers rely on delta hedging every day because it allows them to manage large books of options positions without being overexposed to one-sided moves.

What Is Delta Hedging?

Delta hedging is the process of neutralizing an option’s delta by taking an opposite position in the underlying asset. The objective is to remain delta-neutral, where the portfolio value does not fluctuate sharply with small price changes.

Delta measures the rate of change of an option’s price relative to the underlying. A call option with delta 0.5 increases by about Rs.0.50 for every Rs.1 rise in the stock. If a trader holds one such call (lot size 100 shares), the position delta is +50. To hedge, the trader sells 50 shares of the stock. The net delta becomes zero, and the position is now insulated from small moves.

This hedge is not static. As stock price moves, delta shifts due to gamma. For example, if the stock rises, the call delta might move to 0.7. The position delta is now +70, so the trader must sell an additional 20 shares to stay neutral. This ongoing adjustment makes delta hedging a dynamic process.

The aim is not to eliminate risk entirely but to control directionality, making profit sources like theta (time decay) and vega (volatility exposure) more predictable.

How Does Delta Hedging Work?

Delta hedging works by first calculating delta exposure and then offsetting it with the underlying asset. Traders continuously adjust as delta changes with stock movement.

Step 1: Calculate option delta. Suppose a call has a delta of 0.4 and a put has -0.6.

Step 2: Aggregate total delta. If a trader holds 3 calls (lot size 100), total call delta = 0.4 × 3 × 100 = +120. If the same trader holds 2 puts, total put delta = -0.6 × 2 × 100 = -120. Net delta = 0 (already hedged).

Step 3: Hedge using stock. If the trader had only calls with +120 delta, they would short 120 shares to neutralize.

Step 4: Rebalance dynamically. If the stock rises, the call delta might increase to 0.5. Total call delta = 0.5 × 300 = +150. The hedge must be updated by shorting 30 additional shares.

Dynamic rebalancing is crucial because delta is not constant. It changes with price, time, and volatility. The formula most often used is:

Hedge Ratio=Δ×Contracts×Lot Size\text{Hedge Ratio} = \Delta \times \text{Contracts} \times \text{Lot Size}

By applying this hedge ratio, traders size their offsetting stock positions accurately. The process is continuous, especially in high-gamma environments where delta shifts quickly.

Why Use Delta Hedging Strategy?

Delta hedging is used to neutralize directional bias and profit from other option characteristics. It helps traders and institutions stabilize their portfolios while unlocking opportunities from Greeks.

• Directional neutrality: Prevents one-sided exposure to market moves.
• Theta gains: A delta-neutral short option position earns from time decay.
• Volatility advantage: When volatility rises, hedged positions gain due to vega exposure.
• Risk management: Essential for institutions holding thousands of contracts.

For example, an options desk that sells call options to clients hedges by buying stock. Without the hedge, they would face heavy losses if the stock rallied. With delta hedging, they are insulated from such moves and earn from theta instead.

This makes delta hedging more than a defensive tool; it becomes a structured way to monetize option premiums while minimizing risk.

When to Use Delta Hedging?

Delta hedging is used during periods of uncertainty, in long-dated options, and for managing structured portfolios. It ensures risk stays controlled even when volatility spikes.

• High-volatility events: Earnings, elections, central bank meetings push demand for hedging.
• Long-dated contracts: Delta exposure changes significantly over time, requiring hedging.
• Illiquid options: Traders hedge to avoid sharp swings in thinly traded positions.
• Market makers: Constantly hedge because they cannot afford large exposures.

Suppose a market maker sells 100 put options ahead of earnings. Instead of leaving the book exposed, they delta-hedge with futures. This reduces P/L swings when the announcement hits, while allowing them to profit from inflated premiums.

Who Uses Delta Hedging?

Delta hedging is used primarily by institutions like market makers, hedge funds, and professional desks. Some sophisticated retail traders also apply it with broker platforms.

• Market makers: Hedge continuously to avoid exposure while quoting prices.
• Hedge funds: Run volatility arbitrage strategies using delta-neutral setups.
• Proprietary desks: Trade gamma scalping and theta harvesting with hedged books.
• Retail traders: Advanced individuals with access to Greeks monitoring platforms.

For instance, a hedge fund running a volatility strategy might sell straddles and hedge with underlying futures. Their profits come from time decay, not from predicting market direction. This approach would be impossible without delta hedging.

How Option Greeks Affect Delta Hedging

Option Greeks determine how delta hedging is applied and maintained. While delta is the anchor, gamma, theta, and vega play important roles.

• Delta: Delta measures exposure; dictates hedge size.
• Gamma: Gamma measures how fast delta changes; higher gamma means frequent rebalancing.
• Theta: Theta provides income through time decay; hedgers seek to capture this.
• Vega: Vega reflects volatility exposure; delta hedging does not neutralize this risk.

Greek	Impact on Delta Hedging
Delta	Core hedge measurement
Gamma	Increases adjustment frequency
Theta	Generates profits if hedged
Vega	Leaves volatility risk

A trader shorting options with high gamma needs to rebalance more frequently. Although they collect theta, the cost of rebalancing eats into profits. Understanding these relationships ensures effective hedging.

How Implied Volatility Impacts Delta Hedging

Implied volatility impacts delta hedging by changing option premiums and hedge profitability. Rising IV inflates option values, often increasing hedging challenges.

When Implied Volatility rises, hedged traders face higher costs because option prices expand faster than stock adjustments offset. Vega exposure becomes critical. A delta-neutral portfolio may still lose money if volatility spikes dramatically.

Conversely, in low-IV environments, hedging costs are lower, and theta decay dominates profitability. For instance, traders shorting options ahead of earnings announcements must hedge aggressively due to rising IV, while after the event, hedging becomes cheaper as IV collapses.

The interaction between IV and delta hedging explains why traders combine delta hedging with vega management.

How does Theta Decay impact Delta Hedging?

Theta decay impacts delta hedging by providing a steady source of income if balanced with gamma costs. Selling options and hedging creates positive theta positions.

Theta decay provides daily profits as options lose time value. However, rebalancing costs due to gamma risk reduce these gains. A trader holding short straddles, for example, earns theta but spends money on frequent hedging when prices move.

The key relationship is

• High theta + low gamma: Profitable and stable.
• High theta + high gamma: Income reduced by frequent adjustments.

This trade-off is at the heart of strategies like gamma scalping. Traders aim to manage hedges in a way that theta exceeds adjustment costs.

How to Implement Delta Hedging

Delta hedging is implemented by calculating delta exposure and hedging with underlying or futures. 

To understand delta hedging practically, let’s build a trade position.

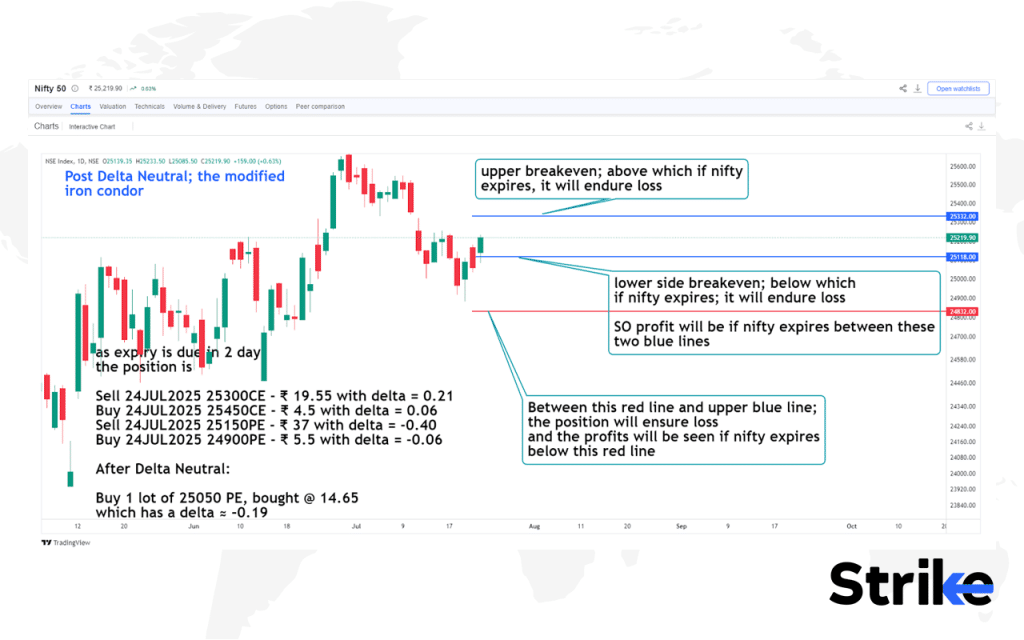
We deploy an Iron Condor on NIFTY expiring in 2 days with the following legs:

• Sell 24JUL2025 25300 CE @ ₹19.55, Delta = +0.21
• Buy 24JUL2025 25450 CE @ ₹4.50, Delta = +0.06
• Sell 24JUL2025 25150 PE @ ₹37.00, Delta = –0.40
• Buy 24JUL2025 24900 PE @ ₹5.50, Delta = –0.06

Net Delta = (–0.21) + (+0.06) + (+0.40) + (–0.06)

= +0.19

This means if NIFTY rises by 100 points per lot, the position gains approximately:

0.19×100×75=₹1,4250.19 \times 100 \times 75 = ₹1,425

To neutralize the delta:

New  Delta=+0.19+(Hedging  Option  Delta)=0New \; Delta = +0.19 + (Hedging \; Option \; Delta) = 0

So we need a hedging option with Delta = –0.19.

From the option chain, 25050 PE has Delta ≈ –0.19.

By buying 1 lot of 25050 PE, the position becomes:

+0.19+(–0.19)=0+0.19 + (–0.19) = 0

Thus, the position is delta-neutral.

• Credit from short 25300 CE and 25150 PE = ₹19.55 + ₹37.00 = ₹56.55
• Debit for long 25450 CE and 24900 PE = ₹4.50 + ₹5.50 = ₹10.00
• Debit for additional 25050 PE = ₹14.65

Net Premium = 56.55 – 10 – 14.65 = ₹31.90 (Net Credit)

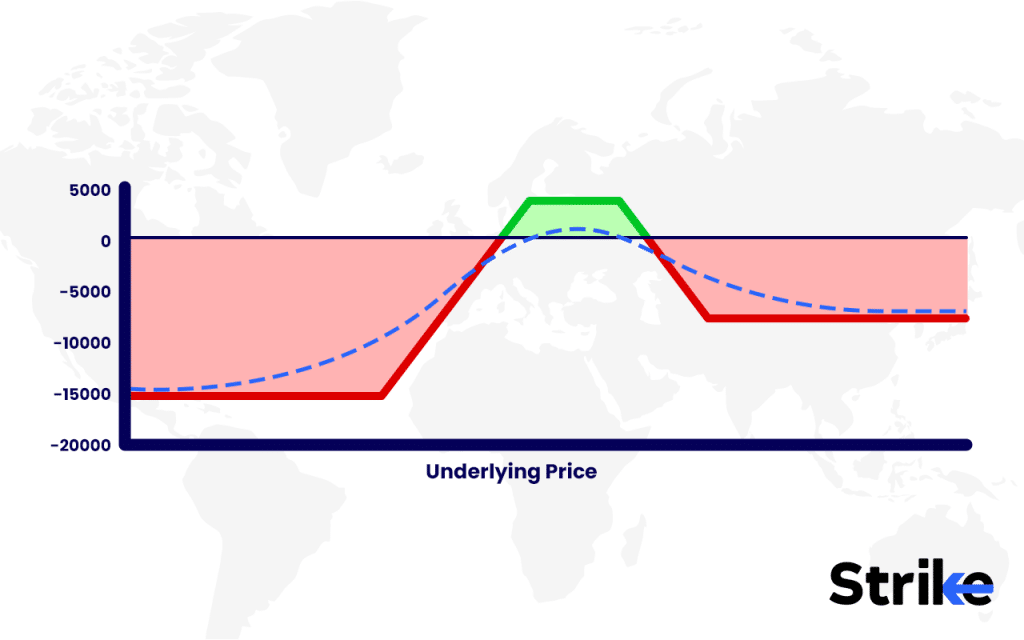
Maximum Profit

Occurs if NIFTY expires between 25150 and 25300 (original iron condor range).

With the long 25050 PE, profit potential extends further on the downside.

Max  Profit=Net  Premium×Lot  Size=31.90×75=₹2,392.50Max \; Profit = Net \; Premium \times Lot \; Size = 31.90 \times 75 = ₹2,392.50

Maximum Loss

Worst-case occurs if NIFTY breaches 24900 or 25450.

Max  Loss=(Spread  Width–Net  Premium)×Lot  SizeMax \; Loss = (Spread \; Width – Net \; Premium) \times Lot \; Size

Spread width = max(25300–25450, 25150–24900) = 150 points

Max  Loss=(150–31.90)×75=₹8,857.5≈₹8,850Max \; Loss = (150 – 31.90) \times 75 = ₹8,857.5 \approx ₹8,850

Breakeven Points

• Upper Breakeven = 25300 + 31.90 = 25332.0
• Lower Breakeven = 25150 – 31.90 = 25118.1

Since we added 25050 PE, there is now a third breakeven at 24832.

• Between 24832 and 25118 → position incurs a loss.
• Below 24832 → position turns profitable theoretically without limit due to the long PE.

After neutralizing delta, the new payoff graph becomes flatter and more controlled, reducing directional risk.

What is an Example of Delta Hedging?

An example of delta hedging can be seen with a long call on Infosys. Suppose Infosys trades at Rs.150 and a call has delta 0.6.

• Position delta = 0.6 × 100 = +60.
• Hedge = short 60 shares.
• Net delta = 0.

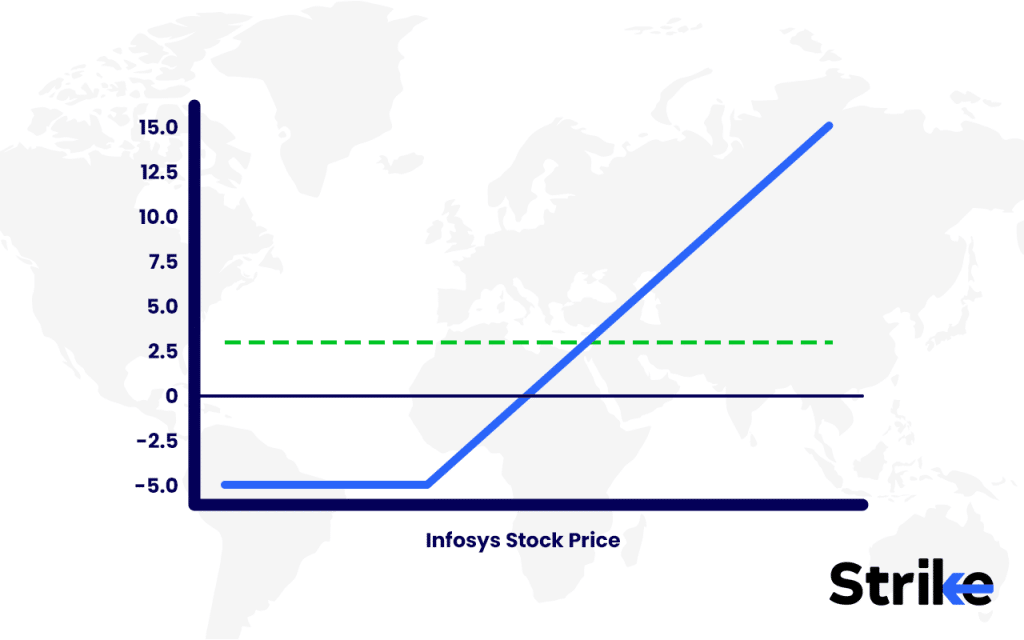
If Infosys rises to Rs.160, delta becomes 0.8. New delta = +80. Adjust by shorting 20 more shares. If Infosys drops to Rs.145, delta falls to 0.4. Exposure becomes +40, so the trader buys 20 shares back.

This adjustment creates a smoother P/L curve compared to an unhedged call. The trader earns from theta decay and volatility changes rather than direction.

What are the Best Platforms for Delta Hedging?

The best platforms for delta hedging are Strike, Sensibull, and TradingView, along with broker apps like Zerodha Kite, FYERS, and Dhan. These platforms give traders access to Greeks, strategy builders, and live rebalancing tools.

• Strike – Known for its clean interface and advanced options analytics. It shows Greeks, payoff diagrams, and simulation features. Its option chain allows delta-neutral setups easily.
• Sensibull – India’s largest options trading platform integrated with brokers. It gives delta values, strategy builders, and alerts for hedge adjustments.
• TradingView – While not broker-specific, it provides powerful charting and data visualization. It helps analyze stock movements needed to anticipate hedge frequency.
• Broker Platforms (Zerodha, FYERS, Upstox, Dhan) – Provide live order execution, option chain access, and margin benefits. While analytics are basic, they integrate with third-party tools like Sensibull for Greeks.

Institutional traders also use Bloomberg and Reuters terminals for real-time delta and gamma data. For retail, Strike and Sensibull stand out because they bring institutional-grade analytics to a simpler interface.

A trader implementing delta hedging needs a platform with three essentials: accurate Greeks, fast execution, and portfolio monitoring. Without these, the hedge becomes ineffective.

What Are the Risks of Delta Hedging?

The risks of delta hedging include gamma risk, transaction costs, slippage, model errors, and exposure to volatility spikes. These risks make the strategy less profitable in certain conditions.

1. Gamma risk: Delta changes rapidly in volatile stocks, forcing frequent rebalancing. High gamma environments increase hedge costs.
2. Transaction costs: Brokerage charges, exchange fees, and STT eat into profits, especially for retail traders.
3. Slippage: Fast-moving markets cause execution at worse prices than intended.
4. Model inaccuracies: Greeks are based on assumptions (like Black-Scholes) that deviate from reality.
5. Tail risk: Sudden crashes or rallies overwhelm delta hedges.

Example: A trader shorting NIFTY options with delta hedge in March 2020 still faced heavy losses because volatility spiked beyond hedge adjustments.

Delta hedging reduces small risks but exposes traders to costs and extreme moves. Balancing theta income against these risks is the core challenge.

Is Delta Hedging Profitable?

Yes, delta hedging is profitable when theta income and volatility edge outweigh hedging costs. Profitability depends on execution skill, frequency, and market conditions.

• Profitable scenarios: Stable markets with moderate moves where theta dominates. Traders shorting options and hedging systematically lock in daily time decay.
• Unprofitable scenarios: High-gamma events (earnings, crashes) where frequent adjustments eat away profits. If the stock whipsaws, rebalancing costs exceed gains.

Institutions often profit because they pay lower transaction fees and hedge in bulk. Retail traders struggle because costs and slippage reduce returns.

Gamma scalping is one way to make delta hedging profitable. Here, traders repeatedly hedge and unhedge, capturing gains from price swings while staying neutral overall. For example, a fund long options hedges with stock and repeatedly adjusts as price fluctuates, earning small scalping gains plus theta.

Profitability in practice depends on balancing income (theta, scalps) versus costs (hedges, slippage, spreads).

How Accurate is Delta Hedging in Practice?

Delta hedging is not perfectly accurate because markets are dynamic and assumptions fail. Accuracy depends on hedge frequency, liquidity, and volatility stability.

Greeks assume continuous hedging, but in reality traders rebalance periodically. Between rebalances, stock moves alter exposure, leading to imperfect neutrality. Liquidity constraints worsen execution.

In stable conditions, delta hedging works well and creates smooth P/L curves. During sudden moves, gaps, or illiquid trading hours, accuracy drops significantly.

For example, a trader hedging Infosys options intraday will manage well during calm trading. But after an overnight gap, the hedge fails since delta shifted outside market hours.

Thus, delta hedging is a tool for risk reduction, not elimination. It works accurately most of the time but breaks during stress events.

Is Delta Hedging Bullish or Bearish?

Delta hedging is neither bullish nor bearish because it aims to stay delta-neutral. The goal is to remove directional bets.

A trader long calls offsets with short stock. A trader short puts offsets with short futures. In both cases, directional risk is neutralized.

This neutrality allows focus on other sources of profit like time decay, volatility, and gamma scalping. For this reason, delta hedging is considered a market-neutral strategy.

However, some traders tilt their hedge to stay slightly long or short delta, expressing a mild directional view while controlling risk.

What is the Difference between Static and Dynamic Delta Hedging?

Static delta hedging adjusts positions occasionally, while dynamic delta hedging requires continuous rebalancing. The choice depends on volatility, costs, and trade objectives.

Feature	Static Hedging	Dynamic Hedging
Frequency	Periodic adjustments	Continuous rebalancing
Cost	Lower	Higher
Risk	Higher directional exposure	Lower directional exposure
Best Use	Low-volatility markets, long-term trades	High-volatility markets, intraday desks

A fund long puts against equity holdings may hedge once a week (static). A market maker quoting options intraday hedges every few minutes (dynamic).

Dynamic hedging is more accurate but expensive. Static hedging is cheaper but less precise. Traders choose based on volatility environment and objectives.

What are the Alternatives to Delta Hedging?

The main alternatives to delta hedging are protective strategies, spreads, gamma-neutral setups, and portfolio diversification. These approaches reduce directional risk without requiring constant rebalancing.

1. Protective (Covered) Calls or Puts
   • Selling calls against a stock position creates downside cushion.
   • Buying protective puts secures insurance without dynamic adjustments.
2. Vertical Spreads
   • Buying and selling options at different strikes caps both profits and losses.
   • Example: A bull put spread on NIFTY locks risk while reducing margin needs.
3. Gamma-Neutral Strategies
   • Iron condors or butterfly spreads balance delta and gamma, reducing hedge frequency.
   • These are often used by retail traders who want defined risk.
4. Portfolio Diversification or Cash Hedging
   • Instead of active hedging, traders allocate across uncorrelated assets.
   • Holding cash, bonds, or gold balances equity risk exposure.

Institutions mix these with delta hedging for layered protection. For retail traders, spreads or protective puts often work better since they eliminate the need for constant rebalancing.