Gamma in Options: What is it, How it Works, Benefits, and Downsides

• Strike
• Options Trading Guide
• Gamma in Options: What is it...

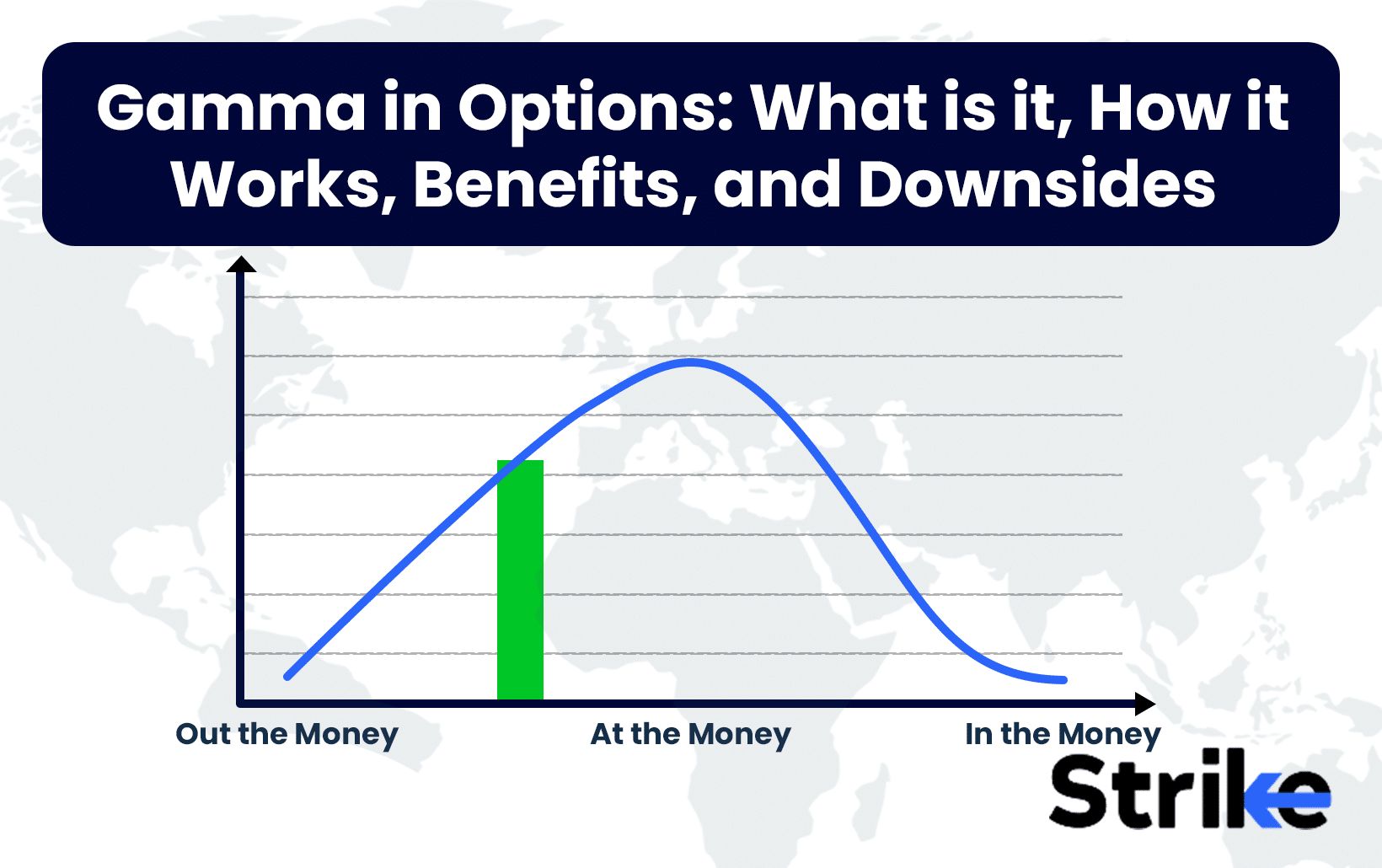
Gamma measures the rate of change in an option’s delta relative to movements in the underlying asset price. Gamma indicates how rapidly delta changes as the asset price moves. Higher gamma means larger delta changes for a given price move.

Gamma is highest when the option is at-the-money as delta changes most rapidly here. Deep in-the-money and out-of-the-money options have lower gamma values. Their deltas do not move as quickly. Gamma is typically larger for options nearing expiration as short-term deltas are more sensitive. For a long call and put, gamma is always positive as delta moves higher as the option goes in-the-money. Gamma helps traders gauge how fast option prices may change around major events or announcements.

Gamma helps size positions knowing delta exposure will change. It allows creating gamma scalping strategies to trade volatility. Gamma indicates higher premium gains from delta changes for at-the-money options. It also warns of accelerating losses from delta working against position.

Gamma is difficult to estimate and model accurately as it depends on many variables. Gamma requires frequent adjustment and monitoring of positions as it shifts. It can result in unexpected volatility and price distortions around strike prices. Gamma also makes hedging and offsetting risk in large portfolios challenging.

What is Gamma in Options?

Gamma is a risk metric that measures the rate of change in an option’s delta relative to changes in the price of the underlying asset. Gamma indicates how much the delta of an option will change given a Rs.1 move in the price of the underlying asset. 

Gamma is an important Greek risk variable for options traders because it helps gauge the speed at which delta changes. The higher the gamma, the more sensitive an option’s delta is to price changes in the underlying. This means higher gamma options experience more significant delta changes for a given change in the underlying asset’s price.

Understanding Gamma

Gamma measures the second derivative of an option’s value relative to shifts in the underlying asset’s price. Mathematically, gamma is expressed as:

Gamma = Delta of Delta 

Or, the rate of change in an option’s delta given a change in the underlying asset’s price.

For example, if an option has a delta of 0.50 and a gamma of 0.05, if the underlying asset increases by Rs.1, the option’s delta increases to 0.55 (a delta change of 0.05). 

Gamma values are always positive for both calls and puts and are typically highest when options are at-the-money. This is because at-the-money options have deltas closest to 0.50, so a small change in the underlying has an outsized impact on the option’s delta.

Gamma is largest for options with short expirations, as there is less time for changes in the underlying price to occur. Longer-dated options have lower gamma since their deltas change less dramatically with shifts in the underlying asset’s price.

Gamma Trading Strategies

Gamma is used in certain main trading methods that traders employ.

• Gamma scalping: This strategy aims to profit from the rapid changes in delta caused by large gamma. Traders look to buy options with high gamma and actively trade the option as the underlying stock moves, benefiting from delta changes.

• Gamma hedging: With this approach, market makers hedge the gamma risk of the options they have sold by buying or selling the underlying asset to maintain a delta neutral position as prices change. This hedges gamma exposure.

• Gamma squeezes: Market makers aggressively buy the underlying when a volatility spike triggers them to hedge their books, becoming collectively short gamma. This push drives further upward price movement, causing a gamma squeeze.

• Negative gamma trading: Some traders aim for negative gamma, meaning they are short options with positive gamma. This benefits from delta declining as the underlying price rises.

Gamma Risks

While gamma might provide trading opportunities to traders, traders must also carefully control the hazards it introduces.

• Gamma risk: Having unhedged positive gamma exposure means the position is exposed to potential adverse delta moves if the stock price declines. Short gamma is risky if the underlying rallies.

• Gamma slippage: The high-frequency delta hedging of large gamma positions lead to hedging losses as the market price moves quickly. Traders experience slippage on their hedges.

• Gamma scalping risks: Attempting to scalp profits from gamma without proper risk management lead to losses if the position delta moves against you unexpectedly.

• Gamma skew risk: Gamma values change as options get further in-the-money or out-of-the-money. This gamma skew requires adjustment of hedge ratios.

What is the purpose of Gamma in Options?

The main purpose of gamma in options trading is to quantify the rate of change in the delta of an option relative to movements in the underlying asset’s price. Gamma is useful information for option traders for numerous reasons.

1. Gauge Delta Sensitivity

Gamma’s primary purpose is to show how sensitive an option’s delta is to changes in the price of the underlying asset. Delta represents the amount an option price is expected to move based on a Rs.1 change in the underlying. 

Gamma measures how much that delta itself will change given changes in the underlying price. The higher the gamma, the more dramatic the delta moves become for a given change in the underlying asset.

For example, an at-the-money call option has a delta of 0.50 and gamma of 0.10. This tells traders that if the underlying stock rises by Rs.1, the call option will increase by Rs.0.50. However, because it has a gamma of 0.10, if the stock price continues rising further, the call option’s delta climbs to 0.60, making it more sensitive to subsequent price changes.

Monitoring gamma gives traders an early warning signal of when delta sensitivity is increasing or decreasing. This helps traders determine when options are becoming more or less responsive to the underlying asset’s price movements.

2. Size Positions Appropriately 

Gamma’s role in showing delta sensitivity makes it a key metric for helping traders properly size option positions. Traders use gamma to determine how many contracts are needed to achieve a desired exposure level to the underlying.

For example, a trader looking for Rs.1000 of exposure could use a lower gamma option requiring 20 contracts to achieve it, or a higher gamma option needing just 10 contracts for the same Rs.1000 delta exposure. In this way, gamma aids position sizing.

3. Assess Gamma Risk

Gamma also plays a central role in highlighting the gamma risk of an options position. Unhedged positive gamma exposure means the position is subject to adverse delta moves if the underlying price declines. Since gamma quantifies the speed of the delta changes, it is a direct measure of gamma risk.

By analysing their gamma levels, traders determine if the risk exposure from rapid delta changes is appropriate for their risk tolerance. The trader hedges delta to bring gamma risk down to acceptable levels. In this way, gamma enables options traders to actively control gamma risk.

4. Identify Trading Opportunities

Sharp spikes or drops in gamma often highlight potential trading opportunities. For instance, a sudden increase in gamma suggests the option’s delta is becoming highly sensitive to the underlying price. 

Traders look to take advantage of this by buying the option to benefit from rapidly expanding deltas as the underlying price moves. Monitoring gamma allows traders to detect when options are becoming more volatile and responsive to the underlying asset’s price action.

5. Manage Gamma Hedging

For options market makers and institutional traders, gamma is essential for determining proper delta hedging levels. As gamma changes, delta hedge ratios need to be adjusted. Gamma informs the frequency and size of delta hedging trades as the underlying price fluctuates.

By quantifying the rate of delta changes, gamma allows market makers to precisely hedge their books and reduce gamma risk through continuous delta adjustments. This helps guide hedging activities and rebalancing.

Why is Gamma important in Options Trading?

Gamma is an extremely important options Greek risk metric that measures the rate of change in the delta of an option relative to movements in the underlying asset’s price. Gamma is critical for options traders to monitor and control for the reasons listed below.

1. Assesses Delta Risk Exposure

Gamma is important because it enables options traders to evaluate their overall exposure to delta risk. Delta represents the estimated change in an option’s price based on a Rs.1 movement in the underlying asset. Gamma quantifies how rapidly that delta exposure is changing as the underlying price moves.

Higher positive gamma means the position’s delta is becoming more sensitive and will move more aggressively for a given change in the underlying. Understanding gamma allows traders to assess if their delta risk is appropriately sized or if it is becoming outsized and unstable. Measuring gamma enables appropriate delta hedging to counterbalance unwanted gamma and delta risk.

2. Guides Position Sizing 

The level of gamma is a key factor for determining proper position sizing in options trading. Traders use gamma to help figure out the number of contracts needed to control the desired delta exposure. 

Lower gamma options will require more contracts to achieve a target delta amount than higher gamma options with the same delta value. Gamma provides information to enhance position sizing precision for delta neutral or directional option trading strategies.

3. Identifies Trading Opportunities

Sudden spikes or drops in an option’s gamma highlight exploitable trading opportunities. For example, a surge in gamma indicates an option is becoming extremely sensitive to the underlying price. Traders look to buy the option to benefit from the rapidly expanding deltas as the underlying price trends.

Monitoring gamma allows traders to detect when options are demonstrating heightened volatility. This signals potential chances to capitalise on large forthcoming price movements.

4. Gamma Scalping

Gamma is the central focus of gamma scalping strategies which aim to profit from the changes in delta caused by sizable gamma. Traders look to buy or sell options with elevated gamma levels and actively trade around them to harvest gains as the deltas shift based on underlying price action. 

The large gamma provides bigger profit potential from delta movements. Gamma is the key factor enabling gamma scalping trading tactics.

5. Hedging Gamma Risk 

Gamma is crucial for quantifying gamma risk so that options market makers properly hedge their books. As overall gamma exposure increases, more active delta hedging is required to offset the higher gamma risk.

By analysing their net gamma levels, market makers know how much delta hedging is needed as underlying prices fluctuate. They buy or sell the underlying asset to maintain delta neutrality. Measuring gamma enables efficient gamma risk hedging activities.

6. Gamma Squeezes

Rapidly rising gamma  also contributes to gamma squeezes in the underlying asset. A volatility spike triggers aggressive buying to hedge deltas when dealers collectively become short gamma, exacerbating upward price momentum and causing a gamma-driven squeeze. 

Monitoring systemic gamma levels can signal conditions that contribute to gamma squeezes, presenting potential trading opportunities.

7. Adjusting Hedging Ratios 

Gamma informs options traders when delta hedge ratios require adjustment. As an option becomes deeper in-the-money or out-of-the-money, its gamma changes, necessitating a modification of delta hedging levels.

Tracking gamma ensures appropriate delta hedging ratios are used, enabling more effective gamma risk management.

8. Gamma Slippage 

While gamma presents trading opportunities, it also poses the risk of gamma slippage. This occurs when the high-frequency rehedging of large gamma exposures results in hedging losses from unfavourable slippage as the underlying price rapidly changes.

Analysing gamma assists in quantifying and preparing for the potential slippage impact on trading strategies. Proper gamma analysis improves risk control.

How does Gamma work?

Gamma measures the rate of change in an option’s delta relative to movements in the underlying asset’s price. Gamma indicates how much an option’s delta will change given a small change in the price of the underlying. This allows traders to evaluate shifting delta risk. 

Gamma is calculated by determining the second derivative of an option’s price based on the underlying asset’s price. The fundamental steps are as follows.

1. Calculate Delta

The first step is to calculate the option’s delta, which represents the change in option price expected from a Rs.1 movement in the underlying asset. For calls, delta ranges from 0 to 1, while for puts it ranges from -1 to 0.

2. Determine Delta at Various Prices  

Next, the delta is calculated at different underlying prices. For example, if the current asset price is Rs.50, deltas can be determined at Rs.49, Rs.50, and Rs.51. This gives a range of deltas at different price points.

3. Subtract Deltas 

The delta values are then subtracted to determine the change between them. For instance, subtracting the delta at Rs.51 from the delta at Rs.50 gives the delta change for a Rs.1 increase in the underlying. Subtracting the Rs.49 delta from the Rs.50 delta yields the delta change for a Rs.1 decrease.

4. Divide by Price Change

The delta change amount is then divided by the change in underlying price, which is Rs.1. This quantifies the delta change per Rs.1 movement in the asset price. 

For example, if the delta change is 0.05 for a Rs.1 price move, the gamma is 0.05.

5. Take Absolute Value 

Since gamma represents sensitivity regardless of the direction the price moves, the absolute value is taken. This makes gamma a positive value.

6. Review Across Prices

Steps 2-5 are repeated at various underlying prices to analyse how gamma changes at different price points and expirations. Gamma will be highest near the current asset price and lower further in/out of the money.

7. Consider Time Decay

Gamma declines as option expiration approaches due to time decay. Less time remaining means less change in delta expected from a Rs.1 price change. Traders must account for time decay when evaluating gamma.

8. Monitor for Trading

Gamma is monitored for spikes and relationships to delta to identify trading opportunities and assess changes in delta risk.Gamma rising increases delta sensitivity, signalling greater volatility.

Gamma is calculated by comparing deltas across different underlying prices, determining the delta change amount, dividing by the price change, and taking the absolute value. Reviewing gamma at various prices and expirations provides insights into changing delta risk.

Higher gamma flags increased sensitivity to the underlying for potential trading signals. By quantifying the delta response to small price moves, gamma allows traders to evaluate shifting risk exposures.

How does Gamma differ from other Option Greeks?

Gamma measures the rate of change in an option’s delta relative to movements in the underlying asset’s price. This makes it distinct from other common Greeks that quantify different elements of risk.

Delta

Delta represents the amount an option’s price is expected to change based on a Rs.1 movement in the underlying asset’s price. It reflects price sensitivity. 

Gamma differs from delta in that it measures the rate of change in delta, rather than just the delta amount itself. Gamma quantifies how rapidly delta is changing, while delta is simply the option’s price exposure.

For example, an option has a delta of 0.50, meaning it will move Rs.0.50 for a Rs.1 change in the underlying. The Rs.0.50 delta amount itself changes quickly with underlying price swings if the option has a gamma of 0.05.

Theta

Theta represents the time decay of an option’s value as expiration approaches. It reflects how much an option’s price declines per day due to the passage of time.

Gamma differs in that it measures sensitivity to underlying price movements, not time decay. However, theta and gamma do interact. As an option moves closer to expiration, theta increases while gamma declines. But they reflect different elements of options risk.

Vega

Vega quantifies an option’s price sensitivity to changes in implied volatility of the underlying asset. It reflects how much an option gains or loses value from a 1% change in implied volatility.

Gamma is distinct in that it looks at sensitivity to the underlying price, not implied volatility. However, oftentimes increased volatility boosts gamma values since prices have potential to move further. But gamma and vega analyse different inputs driving option valuation.

Rho 

Rho indicates an option’s sensitivity to fluctuations in interest rates. It measures the change in an option’s value relative to a 1% move in the risk-free interest rate.

Gamma differs in that it looks at sensitivity to underlying price movements, not interest rates. Rho analyses the impact of rate changes, while gamma examines the asset price.

Gamma provides a unique perspective on options risk by quantifying the rate of change in delta. It differs from other Greeks that measure sensitivity to time decay, implied volatility, and interest rates. While gamma interacts with other Greeks, it specifically analyses the dynamic changes in delta exposure based on underlying price shifts. Monitoring gamma is vital for options traders in conjunction with the other key Greeks. It represents a distinct options risk metric.

How is Gamma used in Options?

Gamma is a significant Greek risk indicator for options that traders regularly watch and use in a variety of ways.

Assessing Risk Exposure

Traders routinely analyse their overall gamma exposure across their options positions. Higher positive gamma indicates greater sensitivity to movements in the underlying asset’s price. Monitoring gamma enables traders to evaluate if their delta risk is appropriate or if it is becoming outsized. 

Managing Unwanted Gamma

Traders look to offset gamma through delta hedging if it gets too high. This involves taking positions in the underlying asset to balance out the rapid rate of change in delta driven by elevated gamma levels. Hedging delta is a common way traders look to control unwanted gamma risk.

Sizing Positions 

Traders use gamma to determine the appropriate number of contracts to control the amount of exposure they take on when initiating new options trades. Lower gamma options require more contracts to achieve a target delta amount than higher gamma options. Gamma assists in precision position sizing.

Timing Entries and Exits

Traders also monitor gamma changes around earnings events or other binary events. A surge in gamma signals the options are becoming very sensitive to movements in the underlying security. This alerts traders to potentially outsized moves and present trading opportunities.

Identifying Opportunities

Sudden spikes or drops in gamma often reflect points where traders look to enter or exit positions to capitalise on shifting premium levels. Rising gamma highlights increased sensitivity, while declining gamma suggests reduced responsiveness to the underlying price.

Gamma Scalping

Some active traders implement gamma scalping strategies specifically looking to profit from gamma changes. This involves buying or selling options with elevated gamma levels and actively trading around the position to benefit from delta moves caused by gamma.

Adjusting Hedging Ratios

As options move deeper in-the-money or out-of-the-money, their gamma value changes. This requires traders to adjust their delta hedging ratios accordingly to account for the shifting gamma risk. Analysing gamma ensures appropriate hedging.

Quantifying Gamma Risk 

Market makers closely monitor their book’s overall gamma exposure. They will actively hedge delta to bring gamma back in line to quantified risk tolerance levels if gamma gets too high on their short options positions. Measuring gamma facilitates dynamic hedging.

Gamma provides a key input for assessing delta risk, managing gamma exposures, identifying opportunities, improving position sizing, timing entry/exits, gamma scalping strategies, adjusting hedge ratios, and quantifying gamma risk. Active options traders rely extensively on gamma analysis across all aspects of the trading process. Understanding and utilising gamma is a vital skill for successful options trading.

Can Gamma be used in the stock market?

No, gamma does not directly apply to analysing regular stock positions, only to options contracts. Gamma specifically measures the rate of change in an option’s delta based on shifts in the underlying stock’s price. Since delta represents sensitivity of the options premium, gamma shows how rapidly that sensitivity changes.

Stocks do not have variables like time value or delta requiring dynamic hedging. Gamma relies on inputs in options pricing models that are not applicable to individual stocks themselves. There is no way to effectively calculate or implement gamma solely in reference to stocks.

Gamma is a significant Greek risk indicator for options that traders regularly watch and use in a variety of ways.

• Large gamma increases signal rising implied volatility expectations, impacting the stock.

• Collectively short gamma in the options market makers contributes to gamma squeezes in the stock when volatility spikes.

• As traders hedge stock positions using options, their hedging needs change based on gamma shifts, indirectly impacting stock flows.

• Gamma’s role in indicating changing delta has some loose analogy to how a stock’s beta shows sensitivity to market moves. 

Gamma is an options-specific Greek that cannot be directly translated to individual stocks themselves. It quantifies a distinct aspect of options pricing behaviour without a direct equivalent in stocks.

How is Gamma in Options Calculated?

Gamma represents the rate of change in an option’s delta relative to movements in the underlying asset’s price. Gamma is derived by determining the rate of change in delta for a small change in the price of the underlying. The steps for calculating an option’s gamma are as follows.

1. Calculate Delta

The first step is to determine the option’s current delta. Delta represents the amount the option price is expected to move based on a Rs.1 change in the underlying asset’s price. Call options have positive deltas between 0 and 1, while put options range from -1 to 0.

2. Determine Delta at Different Prices

After computing the current delta, the trader then calculates what delta would be at hypothetical prices above and below the current market price of the underlying asset. 

For example, if the asset is trading at Rs.50, the trader would determine the option’s delta at incremental prices like Rs.49, Rs.50, and Rs.51. This provides a range of deltas.

3. Subtract the Deltas 

The delta values are then subtracted to quantify the change amount between them. For instance, subtracting the delta at Rs.51 from the delta at Rs.50 gives the change in delta for a Rs.1 increase in the underlying price. This delta change reflects sensitivity.

4. Divide by the Price Change

The delta change amount derived is then divided by the change in underlying price, which is Rs.1. 

For example: (Delta at Rs.51) – (Delta at Rs.50) / Rs.1 change in underlying price.

This gives the rate of change in delta per Rs.1 movement.

5. Take Absolute Value

Since gamma represents sensitivity for both upside and downside moves, the absolute value is taken. This makes gamma positive regardless of the price direction.

6. Review Across Prices

Steps 2-5 are repeated at various hypothetical prices to analyse how gamma changes at different points. Gamma will be highest near the current underlying price and lower when significantly in/out of the money due to the impact on delta.

7. Consider Time Decay

Gamma declines as expiration approaches, so the calculation must account for time decay on the option’s price and delta. Less time remaining means smaller gamma.

Gamma is derived by comparing deltas across different underlying prices, taking the delta change amount, dividing by the price change, and taking the absolute value. This quantifies the rate of change in delta from a small movement in the asset price. The resulting gamma value provides the delta sensitivity rate reflecting how rapidly the option reacts.

What are the factors that may affect Gamma in Options trading?

Gamma represents the rate of change in an option’s delta relative to movements in the underlying asset’s price.There are numerous important aspects that might impact the gamma value of an option.

Underlying Price

An option’s gamma is significantly impacted by how far the current underlying price is from the strike price. Gamma tends to be highest when the option is at-the-money because this is where delta is closest to 0.50 and most sensitive to price changes.

As an option moves further in-the-money or out-of-the-money, its gamma declines because delta becomes less responsive to small price moves. Deep ITM/OTM options have deltas approaching 1 or 0, so changes are minimal. Gamma is largest near the strike price where delta is rapidly changing.

Time to Expiration 

The amount of time remaining until option expiration has a large influence on gamma. Options with longer time until expiry maintain higher levels of gamma all else equal. This is because there is more time for the underlying price to potentially move and impact delta.

As expiration approaches, gamma decays steadily. With less time for the underlying to move, delta becomes less sensitive. Shorter-dated options see their gammas decline significantly heading into expiration. Longer expiries sustain higher gammas for longer periods.

Implied Volatility 

Higher implied volatility of the underlying asset typically increases an option’s gamma. Higher IV signifies greater expected volatility, which means larger potential price swings and greater impact on delta. This results in higher gamma values.

Drops in IV reduce expectations for underlying volatility. This lowers gamma since delta is seen as less responsive with smaller anticipated price movements. High IV environments foster increased gamma.

Strike Price Interval

The distance between an option’s strike price and adjacent strikes impact gamma. Narrower strike intervals mean the option has strikes closely overlapping on either side. This increases gamma near the current price.

Wider strike intervals with fewer overlapping strikes results in lower gamma since delta changes are spread out over a larger price range. Having more closely spaced strikes helps sustain higher gamma.

Does the amount of time until the options expire affect Gamma?

Yes, the time remaining until an options contract expires significantly impacts its gamma value. As the expiration date approaches, gamma decays steadily all else equal due to the decreasing time for the underlying to potentially fluctuate and affect delta.

Longer dated options maintain higher levels of gamma compared to shorter dated options with the same strike and underlying price. This is because there is more time remaining for the underlying asset to experience price movements that could alter the option’s delta. 

With substantial time left until expiry, there is greater potential for the underlying price to move enough to shift delta, so gamma remains elevated.

As expiration nears, gamma drops substantially because there is diminishing time for the underlying to move enough to impact delta. Even large price swings cannot shift delta much with minimal time left.

Therefore, the amount of time remaining directly impacts the option’s gamma. Less time equals lower gamma. Monitoring expiry dates helps traders quantify gamma decay risks and make adjustments to offset declining gamma from expiring contracts.

What does positive and negative Gamma mean?

Gamma represents the rate of change in an option’s delta relative to movements in the underlying asset’s price. Gamma can be either positive or negative depending on the location of the alternatives.

Positive Gamma – Long Options

Being long options contracts creates positive gamma exposure. This means the trader owns options and will benefit from increases in the underlying price.

Positive gamma indicates the option’s delta will increase as the underlying price rises. For a long call, upside moves make the call more in-the-money, increasing delta and premium value. 

The trader’s profits are accelerating with positive gamma since delta rapidly expands as the underlying price increases. The long call gains value faster due to positive gamma.

The long call delta will decrease at an accelerating rate due to positive gamma, lowering premium value if the underlying price declines. But the trader’s risk is limited to the initial premium paid.

Negative Gamma – Short Options

Selling options short creates negative gamma exposure. This means the trader has sold options and will be hurt by rises in the underlying price.

Negative gamma indicates the option’s delta will decrease as the underlying price increases. For a short call, upside moves make the call more in-the-money, increasing delta but lowering premium value.

The trader’s losses accelerate with negative gamma since delta rapidly expands as the underlying price rises. The short call loses value faster due to negative gamma.

The short call delta decreases at an accelerating rate due to negative gamma, raising premium value if the underlying price declines. But losses are unlimited beyond the initial credit received. 

Does Gamma in Put Options always positive?

No, gamma is not always positive for put options. While calls always have positive gamma values, puts have either positive or negative gamma depending on whether the trader is long or short the put contract.

For long puts, gamma will be positive. This means as the underlying price declines, the put option’s delta will increase at an accelerating rate, benefiting the long put position. 

So for traders who are long puts, gamma is positive, similar to long calls. The put gains value faster as the underlying drops due to expanding delta from positive gamma.

However, for short put positions where the trader has sold the put contract, gamma will be negative. As the underlying price declines, the short put delta increases at an accelerating pace, harming the short put trader.

With negative gamma on a short put, the position loses value faster as the underlying drops due to rapidly increasing delta exposure. The accelerating losses represent negative gamma.

Since gamma represents either profit acceleration or loss acceleration depending on the position, puts inherently have both positive and negative gamma exposures.

Is Gamma in Call Options negative?

No, gamma is not negative for outright long call option positions. Gamma represents the rate of change in the option’s delta based on movements in the underlying asset’s price. For long call options, gamma is always positive. 

A positive gamma means as the underlying price increases, the call option’s delta will increase at an accelerating rate. This benefits the long call position since the position gains value faster with rising deltas.

So for outright long call positions, gamma is inherently positive, not negative. The trader profits from the call option becoming more sensitive to the underlying price through positive gamma.

However, short call positions where the trader sells the call options take on negative gamma exposure. As the underlying rallies, the short call delta increases at an accelerating pace due to negative gamma, harming the short call trader.

But for most traders who are simply long call option contracts, gamma remains positive, not negative. The accelerating deltas boost the value of the long call as the underlying price rises.

What is Gamma Hedging?

Gamma hedging involves continuously buying or selling the underlying asset to maintain a delta neutral position as the asset’s price fluctuates. The goal is to hedge the gamma risk resulting from changes in the options portfolio’s delta.

How Gamma Hedging Works

Gamma represents the rate of change in the delta of an option or overall portfolio. As gamma increases, delta becomes more sensitive. This introduces risk if delta moves against the trader’s position.

To hedge this gamma risk, traders offset the changing delta by taking positions in the underlying asset. As the asset price rises, short gamma positions buy the underlying to reduce net positive delta. Long gamma positions sell the underlying to offset increasing negative delta.

By continuously rehedging delta, the portfolio maintains a neutral exposure as prices move. This provides protection against gamma risk.

Purpose of Gamma Hedging 

The main goals and importance of gamma hedging include:

• Reducing gamma risk: Gamma hedging aims to directly offset the accelerating delta created by gamma to remain delta neutral. This smoothes out gamma risk.

• Allow larger positions: Hedging gamma enables traders to hold larger options positions without taking on large directional exposure from changing deltas.

• Define risk parameters: Gamma hedging keeps gamma risk within predetermined tolerance levels by dynamically trading the underlying.

• Lock in profits: As options prices change, hedging allows profits to be locked in rather than facing directional risk from delta fluctuations.

• Precision hedging: Gamma informs how many shares are needed to hedge at any moment based on sensitivity. This enables precise hedging.

• Portfolio protection: Gamma hedging protects entire portfolios against adverse swings stemming from gamma-related delta changes.

Gamma hedging is an important tool for options market makers, institutional traders, and large investors to mitigate gamma risk. It facilitates larger options positions by smoothing out delta fluctuations through continuous hedging. The precision offered by gamma metrics enables effective defensive portfolio management.

What is a good Gamma in Options?

There are no definitive thresholds for what constitutes a “good” gamma value. What represents good or bad gamma depends significantly on the trader’s strategy, risk tolerance, and portfolio objectives.

• For options buyers seeking leverage, higher gamma is often desirable as it provides greater sensitivity to underlying price movements. This allows small moves in the asset to be amplified into potentially large returns from changing premium values. Some traders look for gamma values between 0.05 to 0.10 for enhanced leverage potential.

• For options sellers and writers, lower gamma is generally preferable as it limits exposure to adverse underlying price swings. Writers often aim to keep gamma below 0.05 so position delta doesn’t change too rapidly. This reduces gamma risk when selling options.

• Options with strikes near the current asset price exhibit the highest gamma levels, frequently around 0.07 to 0.10. For traders looking to capitalise on volatility, this zone provides an attractive balance of sensitivity and risk management.

• Very high gamma over 0.10 indicates extreme sensitivity that could introduce unmanageable risks without proper hedging. Traders must determine if this elevated gamma aligns with their risk tolerances.

• Meanwhile, low gamma under 0.01 suggests minimal price sensitivity that does not justify holding the options position unless the goal is limited directional exposure.

• Gamma decay ahead of option expiration rapidly changes the outlook for a position’s sensitivity. Traders must adjust their gamma targets accordingly when expiry approaches.

The desirable gamma amount depends heavily on each trader’s specific trading strategy, timeframe, portfolio objectives, and risk management approach. There are no one-size-fits-all good or bad gamma levels. Active gamma monitoring enables dynamically determining if the amount of leverage and risk exposure remains optimal.

What option has the highest Gamma?

At-the-money (ATM) options generally have the highest levels of gamma. Gamma represents the rate of change in an option’s delta relative to movements in the underlying asset’s price.

Delta is most sensitive to price changes when the option is at-the-money, as the strike price equals the current market price. ATM options have a delta near 0.50, meaning a high probability of finishing in-the-money.

With delta in the midst of its most sensitive zone around a 0.50 probability, any small shifts in the underlying price significantly impact delta. This results in higher gamma values for ATM options.

The further into-the-money or out-of-the-money an option moves, the lower its gamma becomes. Deep ITM/OTM options have deltas approaching 1 or 0, meaning minimal sensitivity to price moves.

Therefore, options closest to at-the-money with deltas near 0.50 exhibit the highest gamma levels, generally between 0.07 to 0.10. This zone provides the greatest sensitivity.

While high gamma boost profits from small underlying moves, it also exposes traders to larger losses if prices trend against them. Appropriate risk management is vital when trading high gamma options.

What option has the lowest Gamma?

Deep out-of-the-money (OTM) and deep in-the-money (ITM) options generally have the lowest levels of gamma. 

Gamma represents the rate of change in an option’s delta relative to movements in the underlying asset’s price. Delta is least sensitive to price changes when the option is deep OTM or ITM.

For deep OTM options, delta is near zero, as the strike price means a very low probability of finishing in-the-money. Small asset price movements have minimal impact on deep OTM deltas.

Meanwhile, deep ITM options have a delta near 1, as the strike price implies a very high probability of expiring in-the-money. But further underlying price changes barely shift the deep ITM delta.

With deltas at extremes of either 1 or 0, gamma falls very low for both deep OTM and ITM options, generally below 0.01. This reflects minimal sensitivity to the underlying price.

Lower gamma reduces potential profits but also curbs potential losses from adverse price swings. For options sellers, lower gamma is generally advantageous as it limits gamma risk.

However, for options buyers seeking leverage, lower gamma diminishes the profit potential from volatility expansion. Higher gamma amplifies gains from favourable price moves.

What are examples of Gamma in Options?

Here are three instances of gamma levels and their effects in options trading.

1. High Gamma Example 

An SPY 340 call option has a delta of 0.60 and gamma of 0.12 with SPY at 342. The high 0.12 gamma means that if SPY rises Rs.2 to 344, the call option’s delta increases around 0.24 to 0.84. The high gamma amplifies the call value’s sensitivity to SPY’s price move.

2. Low Gamma Example

A TSLA 900 put option has a delta of -0.05 and gamma of 0.01 with TSLA at 800.The low 0.01 gamma means that if TSLA drops Rs.5 to 795, the put’s delta only increases about 0.05 to -0.10. The minimal gamma limits sensitivity to TSLA’s downward move.

3. Gamma Hedging Example 

A trader has a portfolio with a delta of +100 and gamma of +50.The portfolio’s delta increases roughly +500 to +600 if the S&P drops 10 points to 2790 due to the +50 gamma. To hedge this new long delta exposure, the trader needs to sell roughly 500-600 shares of SPY. Active hedging aims to keep the portfolio delta neutral as gamma changes.

Higher gamma means larger delta changes from underlying price movements, while lower gamma mutes sensitivity. Monitoring gamma enables traders to actively manage portfolio risk and hedge changing deltas when necessary. Gamma’s role in amplifying or dampening volatility is a key consideration for options traders.

What are the Benefits of Gamma in Options?

Here are some of the primary advantages of using gamma in options trading.

• Assesses delta risk exposure: Gamma enables evaluating overall exposure to shifting delta risk. Higher gamma means increased delta sensitivity.

• Guides position sizing: Gamma helps determine the number of contracts needed to control desired delta exposure for directional or non-directional trades.

• Identifies trading opportunities: Spikes or drops in gamma often signal potential profitable trading opportunities.

• Quantifies “gamma scalping” potential: High gamma options present potential opportunities to profit from delta changes through gamma scalping approaches.

• Informs hedge adjustments: Changing gamma levels signal when delta hedge ratios need to be rebalanced.

• Allows larger positions: Hedging gamma enables taking larger options positions without unbalanced directional exposure.

• Defines risk parameters: Gamma helps set defined risk tolerance thresholds that can be managed through delta hedging.

• Smooths portfolio volatility: Hedging gamma helps offset the portfolio volatility that could result from delta fluctuations.

• Enables gamma squeezes: Rapidly rising gamma can contribute to gamma squeezes, creating trading opportunities.

Monitoring gamma provides traders with insights into changing delta exposure and sensitivity for making better risk management decisions and identifying potential trades.

What are the Downsides of Gamma in Options?

• Gamma risk: Unhedged positive gamma means adverse delta moves if underlying price declines. Short gamma risks unexpected losses if prices rally.

• Volatility drag: Rapid delta adjustments from high gamma can create “whip saw” volatility drags as exposure changes.

• Gamma slippage: Frequent rehedging large gamma can lead to slippage losses as underlying prices move swiftly.

• Vega/gamma misalignment: Losses might occur when volatility expectations change against gamma exposures.

• Gamma scalping risks: Attempting to trade pure gamma without balancing risks can lead to losses from unfavourable delta moves.

• Hedging costs: There are explicit transaction costs associated with continuously gamma hedging through trading the underlying.

• Gamma skew: Changing gamma at different delta strikes requires adjustments to hedge ratios. Skew adds complexity.

• Unwinding impact: Large gamma positions being unwound can negatively impact broader market prices and volatility. 

• Gamma mismatch: Offsetting positive and negative gamma exposures is complex and still leaves residual risk.

• Portfolio drag: Excessive unhedged gamma trading can result in unwanted portfolio volatility drag.

While gamma presents opportunities, traders must actively measure and manage associated risks. Ignoring gamma exposure can lead to unexpected losses as deltas swing.

What is the difference between Gamma and Delta in Options?

Delta 

• Delta represents the estimated change in the price of an option given a small change in the price of the underlying asset.

• It reflects the sensitivity of the option’s premium value to shifts in the underlying price. 

• Delta ranges from 0 to 1 for calls and 0 to -1 for puts. A 0.50 delta means a 50% chance the option expires in-the-money.

• Delta indicates the amount of directional exposure created by the options position.

Gamma

• Gamma measures the rate of change in the delta based on movements in the underlying asset’s price. 

• It quantifies how rapidly the option’s delta changes given changes in the underlying price.

• Gamma is always positive and is highest when options are at-the-money near a 0.50 delta.

• Gamma represents the speed of delta changes, not just the delta amount itself.

Key Differences

• Delta measures absolute price exposure, gamma measures rate of delta change.

• Delta is positive or negative based on call/put, gamma is always positive. 

• Delta quantifies directional exposure, gamma quantifies delta risk.

• Delta is highest deep ITM/OTM, gamma peaks near-the-money.

• Delta is a first-order derivative, gamma is a second-order derivative.

• Traders use delta for exposure targeting, gamma for hedging and risk management.

Delta represents outright exposure to the underlying price while gamma indicates how quickly that exposure changes through time. Monitoring both delta and gamma enables more complete options trade analysis and risk management.