Rho is an option Greek that impacts the option of securities. Rho helps understand how interest rate fluctuations can impact options’ pricing and hedging. Option Greeks are some of the financial measures that impact an option instrument’s prices and value in the financial market. Rho was developed after the development of Black-Scholes-Merton model in the early 1970s, when it was felt that interest rates do also impact the option demand and supply in the market.
This article will explore the usage, and relevance, and solve the intricacies of rho in the option instruments by different definitions, calculations, and comparisons of rho with the market dynamics.
What is Rho in Options Trading?
Rho is an option greek that measures the sensitivity of the price of options relative to the changes in the risk-free rate of return. This rate is the rate of return of government bonds and T-bills, considered the safest investment. Rho is expressed as the amount of money an option instrument loses or gains with a 1% change in the interest rates.
So, why are options prices and interest rates connected, measured in the form of an option Greek named rho? The answer is interest rates can have an impact on an option’s value as interest rates can alter the cost of carrying an option over time. Interest rates affect the longer-term options more than the short-term options.
How Rho is used in Trading?
Rho is used by traders and investors to assess how the changes in interest rates might affect the value and price of the option positions. Options positions are generally taken to hedge the risk against the investment positions. Rho helps in strategic planning, hedging against interest rates, and managing the risk sensitivity overall of a portfolio.
Positive Rho
Positive rho refers to the characteristic of rho where the option’s price increases as the interest rates increase. Call options generally have a positive rho. This means that an increase in the interest rates increases the value of the call option. The reason is, that higher interest rates make it costly to hold cash instead of investing it in the underlying asset. For example, if the interest rates increase from 5% to 6%, the expected returns from the asset will increase, and this makes a loss of an additional 1% if the cash is not invested into the asset.
Negative Rho
Negative rho is associated with the characteristic where the option price decreases with an increase in interest rates, and vice-versa. Put options usually have a negative rho. An increase in the interest rates decreases the value of a put option. This occurs because higher interest rates decrease the chances of negative returns from the asset, reducing the present value of the put option, and making the put option less attractive.
How Rho is calculated?
Rho is calculated using the mathematical models, the most common being the Black-Scholes model. The formula of the option depends on the type of the option, whether it is a call or a put option, and variables such as asset price, expiry time, risk-free rate of interest, and strike price.
Rho for Call Options

Where:
- C is the price of call option
- K is the strike price of the option
- T is the time to expiry (in years)
- R is the risk free interest rate (compounding)
- N(d2) is the cumulative distribution function of the standard normal distribution evaluated at d2.
- E is the base of natural logarithm (appx. equal to 2.71)
Rho for Put Options

Where:
- P is the price of the put option.
- The other variables (K, T. r, e, N (d2))
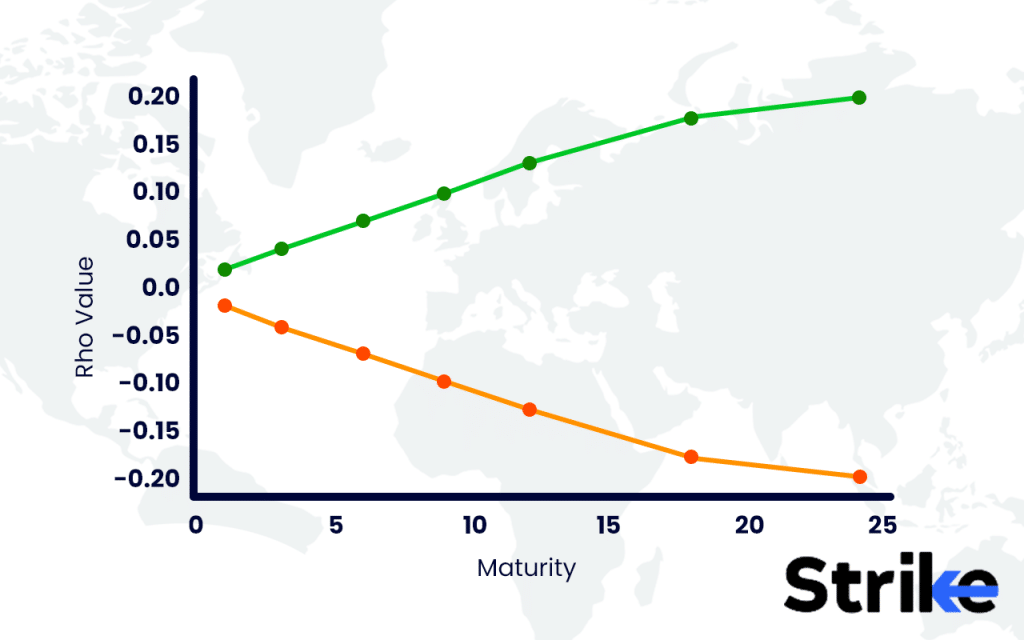
The higher stock price and the longer expiry period, tend to a greater sensitivity to the interest rates, which results in higher rho value for such option contracts. The cost of carrying a Rs. 1000 stock position over time will be greater than the cost of carrying a Rs. 200 stock, and the cost of money increases with a longer time frame. It is also known that interest rates may be different for different clearing houses and brokerage firms.
How Does Rho Impact the Option Price?
Rho’s impact on the option price is generally greater with the time of expiry and the strike price. With longer time options to expiry, deep-in-the-money options have a higher sensitivity to rho, meaning that even a small change in the interest rates can lead to a substantial amount of price adjustment. Conversely, Rho has a minimal effect on short-term option contracts. In such contracts other factors. like theta and delta are more influential.
Rho and Call Options
For the call options, rho is generally positive. Rho is positive for purchased calls because higher interest rates increase the call value or premium. Long calls give the right to purchase the stock, usually, the cost of that right is lesser than the fully exercisable value. The difference between these two numbers can be deposited into an interest-bearing account. In a higher interest rate environment, this makes the call option more favorable.
For example:
Stock SBIN is priced at Rs. 800.
Interest rate – 5%
Call option rho – 0.45 @ 5% interest rate
Expiry of option – 1 year
Buying stock value – 750 shares at 800 costs Rs. 6, 00,000.
Buying call option – Buy 1 Rs. 800 call at a premium of Rs. 100 (lot size – 750) costs Rs. 75,000.
The total exercisable value of this option is 6,00,000. The cost of purchase is 75,000. Rest 5,25,000 can be deposited for interest. Say the interest rates increases from 5 to 6%. The premium increased from 100 to 100.45. As the interest rates increase, it reflects positively on the long-term call options.
Rho and Put Options
For the put options, rho is generally negative as the higher interest rates decrease the put premiums. As interest rates rise, the value of the option tends to decrease because the present value of the exercise price of the asset decreases, making the put less attractive.
A long put gives the buyer the right to sell the shares at a predetermined price for the option premium which results in a debit. Similar to the call option, the seller can buy a long put, and deposit the rest amount into a bank for interest earning. It makes long puts less attractive in high inteRs.t rate environment.
For example:
Stock SBIN is priced at Rs. 800.
Interest rate – 5%
Put option rho: (-) 0.55 @ 5% interest rate
Expiry of option – 1 year
Buying stock value – 750 shares at 800 costs Rs. 6,00,000.
Buying call option – Buy 1 Rs. 800 call at a premium of Rs. 90 (lot size – 750) costs Rs. 67,500.
The total exercisable value of this option is 6,00,000. The cost of purchase is 75,000. The rest of the 5,25,000 can be deposited for interest. Say the interest rates increase from 5 to 6%. The premium decreases from 90 to 89.55. As the interest rates increase, it reflects positively on the long-term call options.
The total exercisable value of this option is 6,00,000. The cost of purchase is 75,000. The rest 5,25,000 can be deposited for interest. Say the interest rates increase from 5 to 6%. The premium increased from 100 to 100.45. As the interest rates increase, it reflects positively on the long-term call options.
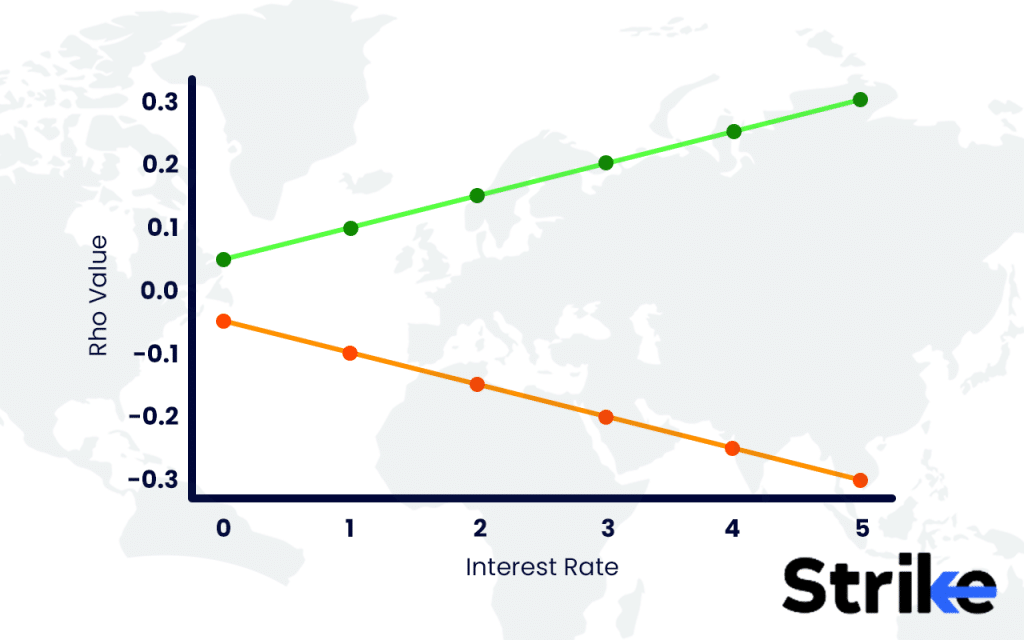
Rho and Interest Rates
Rho is directly linked with the change in interest rates, such as government bonds or T-Bills. Changes in the monetary policy or macroeconomic environment can lead to changes in the interest rate values, which in turn affects rho, consequently the value of an option.
What Are the Applications of Rho in Option Trading?
Rho is an important measure for option traders, portfolio, and hedge fund managers to understand the change in interest rates and its impact on option prices, and they can better manage their heavy funds.
Relevant Time to Use Rho
Rho becomes increasingly important in the periods of anticipation of interest rate changes. Long-term options are particularly affected by changes in monetary policy change, making rho a critical factor in such situations, and has the highest importance of rho in option prices. In a rising interest rate environment, trades favor call options due to their positive rho, expecting these options to increase in value.
For example – in the present time (August 2024), economies all over the world are mulling over interest rate cuts and increasing the money supply to cater to the slowing down of economies. The United States of America is expected to cut Fed interest rates by 3% from the current 5.25% gradually over a period of 2 years. This is the most relevant time for investors in the United States of America to examine the value of rho in their options strategies.
A cut in the interest rates will decrease the premium of options. In the above examples, if the rate is decreased from 5% to 4%, the call option premium will decrease by 0.45, as a 1% decrease will lead to a decrease of 0.45. The SBIN call option then becomes 99.55 from 100.
Integration of Rho with Other Options Greeks
Traders use rho with other option Greeks like delta, theta, gamma, and Vega to get a complete picture of the price estimation and prediction of future prices and risks associated with the option. This helps in building strategies that are more relevant in particular times, like changing market and economic conditions.
For example: In times of high volatility, a trader checks the theta decay rate on options. During the times of election, the volatility index becomes more important to check which makes theta decay per day more important, as well as rho because a change in government can make changes in interest rates also as a part of different policy implications.
Trading In Rising Interest Rates Using Rho
Rising interest rates provide a more lucrative and safe return option for investors. Say, the 5% interest rate when changes to 6%, there is a benefit of 1% return. The investor who has bought a call option (in place of depositing in the Central Bank) will be compensated by increased rho (and thereby increased premium on call) against the lost opportunity of earning that extra 1% interest.
How Rho is Different from Other Option Greeks
Option Greeks are the risk parameters that measure the various risks attached to the option instrument. Options Greeks are those measurable factors that change the price of the option instrument. A comparison of primary option Greeks with rho is defined below.
- Rho vs. Delta: Delta is a measure of change in the option’s price or premium which results from the change in the price of the underlying asset. On the contrary, rho measures the sensitivity to interest rate changes.
- Rho vs. Theta: Theta measures the fall in price (known as price decay) as time passes, as an option comes with an expiry date. As time passes, the theta value comes down. Rho is concerned with the influence of interest rate changes.
- Rho vs. Vega: Vega measures the risk of changes in the implied volatility or the near-term expected volatility of the underlying asset price. Rho focuses on the impact of interest rate variation.
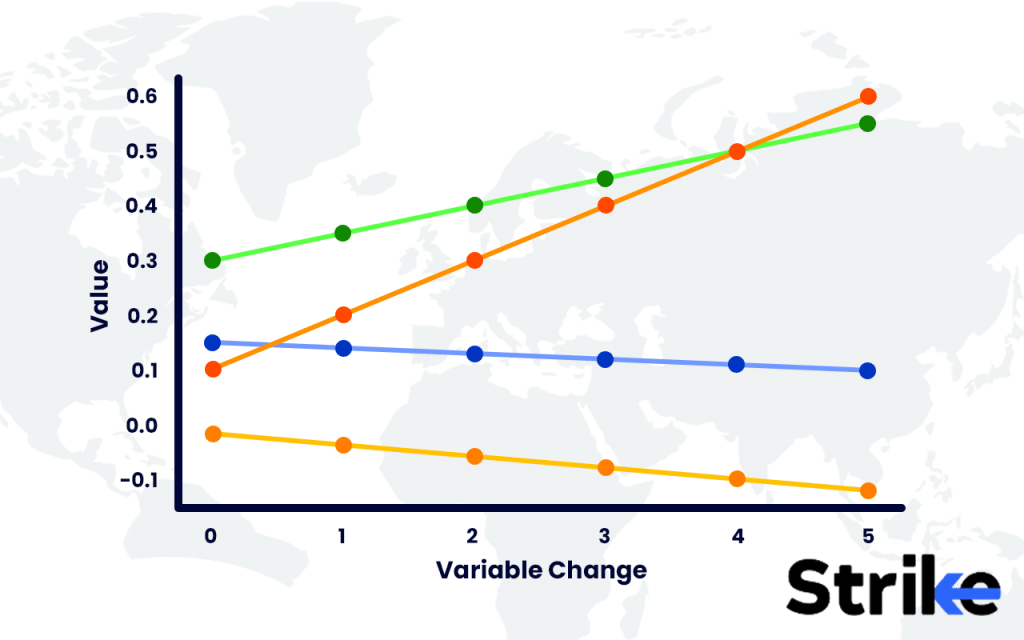
This is elaborated with the below example.
Stock – NHPC ltd
Current price- RS. 100
Strike price- 105
Expiry- 30 days
Volatility – 20%
The risk-free rate of return – 5%
With this information, if the delta is 0.6, for every Rs. 1 increase in the stock price, the option price will increase by Rs. 0.60.
If gamma is 0.05, with the increase of Rs. 1 in stock price, delta will increase by 0.05
If the theta is (-) 0.02, the option price will decrease by Rs. 0.02 each day, assuming all other factors remain the same.
If the Vega is 0.10, a 1% volatility will increase the price of the option by Rs. 0.10.
If rho is 0.05, a 1% increase in the inteRs.t rate will increase the price of the option by 0.05.
How to Monitor Rho?
- Best platforms to track rho: Most advanced trading platforms like Trading View give real-time data on option Greeks including rho. These trading platforms allow users to analyse and monitor the overall risks associated with the option which is reflected with these option Greeks.
- Setup alerts for rho: Traders can set alerts for significant changes in the rho on such platforms. This is particularly useful when large portfolios are managed, and slight differences in option price amount to a considerable money or when economic policy changes are expected.
What Are The Common Myths of Rho?
- Misunderstanding impacts of interest rate: one common myth about rho is that it is relevant only in extreme interest rate change environment. But in fact, even small changes in rho can have a considerable impact on the price of long-term options.
- Role in short-term options: Another myth is that rho has no impact on short-term option instruments. This is not true during times of volatile interest rates, who has a considerable impact even on short-term options.
What Does a High Rho Indicate?
A high rho indicates that the option value is highly sensitive to the changes in the interest rates. This is typically seen in the long and deep-in-the-money options with a long time to expire. Traders who are holding such options need to carefully observe the interest rate perspectives and potential changes.
How Rho Changes Near Options Expiry?
As the option approaches its expiry, rho generally comes down because the remaining time value of an option decreases. Lesser time to expiry means lesser risk of interest rate changes. This entails that interest rate changes are now less significant compared to other factors. Of the options like delta movement or theta decay of the underlying asset.











No Comments Yet.