Statistical analysis refers to the collection, organization, interpretation, and presentation of large volume of data to uncover meaningful patterns, trends, and relationships. Statistical analysis utilizes mathematical theories of probability to quantify uncertainty and variability in data.
The process of statistical analysis begins with data collection, where relevant data is gathered from various sources such as historical records, surveys, and experiments. This raw data is then organized into a comprehensible format. The next phase is known as descriptive analysis, and the sample data’s characteristics are summarized and described. This is often done using visualizations and summary statistics such as the mean, median, variance, and standard deviation. Hypothesis testing follows, in which statistical tests and probability distributions are used to either accept or reject hypotheses.
These hypotheses pertain to the true characteristics of the total population, and their acceptance or rejection is based on the sample data. Then comes regression analysis, which is used for modeling relationships and correlations between several variables. Techniques like linear regression are often employed in this phase to make estimations and predictions. Inferential analysis is the next step, where inferences about the broader population are made. These inferences are based on the patterns and relationships observed within the sample data and are solidified through statistical significance testing. Model validation is carried out to assess the predictive accuracy of the statistical models and relationships. This is done on out-of-sample data and over time to ensure the model’s effectiveness and accuracy in prediction.
What is Statistical Analysis?
Statistical analysis refers to a collection of methods and tools used to collect, organize, summarize, analyze, interpret, and draw conclusions from data. Statistical analysis applies statistical theory, methodology, and probability distributions to make inferences about real-world phenomena based on observations and measurements.
Statistical analysis provides insight into the patterns, trends, relationships, differences, and variability found within data samples. This allows analysts to make data-driven decisions, test hypotheses, model predictive relationships, and conduct measurement across fields ranging from business and economics to human behavior and the scientific method.
Below are the core elements of statistical analysis. The first step in any analysis is acquiring the raw data that will be studied. Data is gathered from various sources including censuses, surveys, market research, scientific experiments, government datasets, company records, and more. The relevant variables and metrics are identified to capture.
Once collected, raw data must be prepared for analysis. This involves data cleaning to format, structure, and inspect the data for any errors or inconsistencies. Sample sets may be extracted from larger populations. Certain assumptions about the data distributions are made. Simple descriptive statistical techniques are applied to summarize the characteristics and basic patterns found in the sample data. Common descriptive measures include the mean, median, mode, standard deviation, variance, frequency distributions, data visualizations like histograms and scatter plots, and correlation coefficients.
Statistical analysis, integral to business, science, social research, and data analytics, leverages a variety of computational tools and methodologies to derive meaningful insights from data. It provides a robust quantitative foundation that enables organizations to make decisions based on hard facts and evidence, rather than intuition. A critical component of this analysis is the use of various chart types to visually represent data, enhancing understanding and interpretation.
Bar charts are commonly used to compare quantities across different categories, while line charts are preferred for displaying trends over time. Pie charts are useful in showing proportions within a whole, and histograms excel in depicting frequency distributions, which are particularly useful in statistical analysis. Scatter plots are invaluable for identifying relationships or correlations between two variables, and box plots offer a visual summary of key statistics like median, quartiles, and outliers in a dataset. Each type of chart serves a specific purpose, aiding researchers and analysts in communicating complex data in a clear and accessible manner.
How Does Statistical Analysis Work?
Statistical analysis works by utilizing mathematical theories of probability, variability, and uncertainty to derive meaningful information from data samples. Applying established statistical techniques help analysts uncover key patterns, differences, and relationships that provide insights about the broader population.
For analyzing stocks, statistical analysis transforms price data, fundamentals, estimates, and other financial metrics into quantifiable indicators that allow investors to make strategic decisions and predictions. Here is an overview of the key steps.
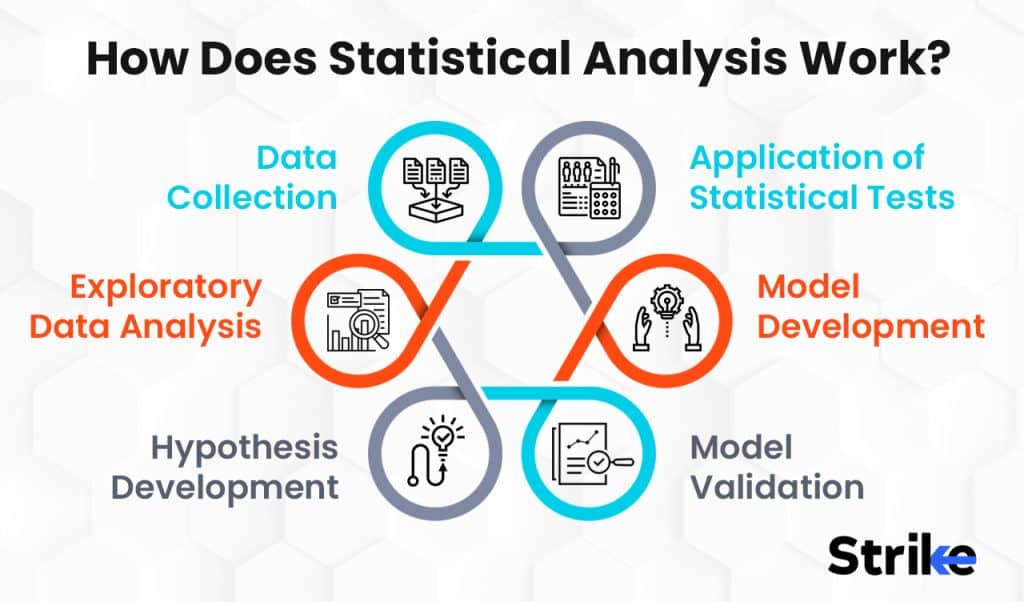
Data Collection
The first requirement is gathering relevant, accurate data to analyze. For stocks this includes historical pricing data, financial statement figures, analyst estimates, corporate actions, macroeconomic factors, and any other variable that could impact stock performance. APIs and financial databases provide extensive structured datasets.
Exploratory Data Analysis
Once data is compiled, initial exploratory analysis helps identify outliers, anomalies, patterns, and relationships within the data. Visualizations like price charts, comparison plots, and correlation matrices help spot potential connections. Summary statistics reveal normal distributions.
Hypothesis Development
Statistical analysis revolves around developing hypotheses regarding the data and then testing those hypotheses. Technical and fundamental stock analysts generate hypotheses about patterns, valuation models, indicators, or predictive signals they believe exist within the data.
Application of Statistical Tests
With hypotheses defined, various statistical tests are applied to measure the likelihood of a hypothesis being true for the broader population based on the sample data results. Common statistical tests used include t-tests, analysis of variance (ANOVA), regression, autocorrelation, Monte Carlo simulation, and many others.
Model Development
Significant statistical relationships and indicators uncovered in testing is further developed into quantitative models. Regression analysis models correlations between variables into predictive equations. Other modeling techniques like machine learning algorithms also rely on statistical theory.
Model Validation
The predictive accuracy and reliability of statistical models must be proven on out-of-sample data over time. Statistical measures like R-squared, p-values, alpha, and beta are used to quantify the model’s ability to forecast results and optimize strategies.
Statistical analysis makes extracting meaningful insights from the vast datasets related to stocks and markets possible. By mathematically testing for significant relationships, patterns, and probabilities, statistical techniques allow investors to uncover Alpha opportunities, develop automated trading systems, assess risk metrics, and bring disciplined rigor to investment analysis and decision-making. Applied properly, statistical analysis empowers effective navigation of financial markets.
What is the Importance of Statistical Analysis?
Statistical analysis is an indispensable tool for quantifying market behavior, uncovering significant trends, and making data-driven trading and investment decisions. Proper application of statistical techniques provides the rigor and probability-based framework necessary for extracting actionable insights from the vast datasets available in financial markets. Below are several nine reasons statistical analysis is critically important for researching and analyzing market trends.
Statistical measurements allow analysts to move beyond anecdotal observation and precisely define trend patterns, volatility, and correlations across markets. Metrics like beta, R-squared, and Sharpe ratio quantify relationships.
For example, beta is a measure of a stock’s volatility relative to the market. A stock with a beta of 1 has the same volatility as the market, while a stock with a beta of 2 is twice as volatile as the market. R-squared is a measure of how well a regression line fits a data set. A high R-squared value indicates that the regression line fits the data well, while a low R-squared value indicates that the regression line does not fit the data well. The Sharpe ratio is a measure of a portfolio’s risk-adjusted return. A high Sharpe ratio indicates that a portfolio has a high return for its level of risk.
Statistics allow analysts to mathematically test hypothesized cause-and-effect relationships. Correlation analysis, regression, and significance testing help determine if one factor actually drives or predicts another.
For example, correlation analysis is used to determine if there is a relationship between two variables. A correlation coefficient of 1 indicates that there is a perfect positive correlation between two variables, while a correlation coefficient of -1 indicates that there is a perfect negative correlation between two variables. A correlation coefficient of 0 indicates that there is no correlation between two variables. Regression analysis is used to determine if one variable is used to predict another variable. A regression line is a line that represents the relationship between two variables. The slope of the regression line indicates the strength of the relationship between the two variables. The y-intercept of the regression line indicates the value of the dependent variable when the independent variable is equal to 0. Significance testing is used to determine if the relationship between two variables is statistically significant. A statistically significant relationship is one that is unlikely to have occurred by chance.
Statistical hypothesis testing provides the ability to validate or reject proposed theories and ideas against real market data and define confidence levels. This prevents bias and intuition from clouding analysis.
For example, a hypothesis test is used to determine if there is a difference between the mean of two groups. The null hypothesis is that there is no difference between the means of the two groups. The alternative hypothesis is that there is a difference between the means of the two groups. The p-value is the probability of obtaining the results that were observed if the null hypothesis were true. A p-value of less than 0.05 indicates that the results are statistically significant.
Performance measurement, predictive modeling, and backtesting using statistical techniques optimize quantitative trading systems, asset allocation, and risk management strategies.
For example, performance measurement is used to evaluate the performance of a trading strategy. Predictive modeling is used to predict future prices of assets. Backtesting is used to test the performance of a trading strategy on historical data.
Time series analysis, ARIMA models, and regression analysis of historical data allows analysts to forecast future price patterns, volatility shifts, and macro trends.
For example, time series analysis is used to identify trends in historical data. ARIMA models is used to forecast future values of a time series. Regression analysis is used to forecast future values of a dependent variable based on the values of independent variables.
Statistical significance testing minimizes confirmation bias by revealing which patterns and relationships are statistically meaningful versus those that occur by chance.
For example, confirmation bias is the tendency to seek out information that confirms one’s existing beliefs. Statistical significance testing can help to reduce confirmation bias by requiring that the results of a study be statistically significant before they are considered to be valid.
How Does Statistical Analysis Contribute to Stock Market Forecasting?
Quantitatively testing relationships between variables, statistical modeling techniques allow analysts to make data-driven predictions about where markets are heading based on historical data. Below are key ways proper statistical analysis enhances stock market forecasting capabilities.
In Quantifying Relationships, correlation analysis, covariance, and regression modeling quantify linear and nonlinear relationships and interdependencies between factors that impact markets. This allows development of equations relating variables like prices, earnings, GDP.
In Validating Factors, statistical significance testing determines which relationships between supposed predictive variables and market movements are actually meaningful versus coincidental random correlations. Valid factors is incorporated into models.
In Time Series Modeling, applying statistical time series analysis methods like ARIMA, GARCH, and machine learning algorithms to historical pricing data uncovers seasonal patterns and develops predictive price trend forecasts.
In Estimating Parameters, tools like regression analysis, Monte Carlo simulation, and resampling methods estimate key parameter inputs used in financial forecasting models for elements like volatility, risk premiums, and correlation.
In Evaluating Accuracy, statistical metrics such as R-squared, RMSE, MAE, out-of-sample testing procedures validate the accuracy and consistency of model outputs over time. This optimization enhances reliability.
In Combining Projections, individual model forecasts are aggregated into composite projections using statistical methods like averaging or weighting components based on past accuracy or other factors.
In Reducing Uncertainty, statistical concepts like standard error, confidence intervals, and statistical significance quantify the degree of uncertainty in forecasts and the reliability of predictions.
Trained financial statisticians have the specialized expertise required to rigorously construct models, run simulations, combine complex data sets, identify relationships, and measure performance in order to generate accurate market forecasts and optimal trading systems.
No amount of statistical analysis predict markets with 100% certainty, but advanced analytics and modeling techniques rooted in statistics give analysts the highest probability of developing forecasts that consistently beat market benchmarks over time. Proper statistical application helps remove human biases, emotions, and misconceptions from market analysis and decision-making. In a field dominated by narratives and competing opinions, statistical analysis provides the quantitative, empirically-grounded framework necessary for making sound forecasts and profitable trades.
What Are the Statistical Methods Used in Analyzing Stock Market Data?
Below is an overview of key statistical methods used in analyzing stock market data.
Descriptive Statistics
Descriptive statistics provide simple quantitative summary measures of stock market data. This includes calculations like the mean, median, mode, range, variance, standard deviation, histograms, frequency distributions, and correlation coefficients.

Measures of central tendency like the mean and median calculate the central values within stock data. Measures of dispersion like range and standard deviation quantify the spread and variability of stock data. Frequency distributions through histograms and quartiles show the overall shape of data distributions. Correlation analysis using Pearson or Spearman coefficients measures the relationship and co-movement between variables like prices, fundamentals, or indicators. Descriptive statistics help analysts summarize and describe the core patterns in stock datasets.
Regression Analysis
Regression analysis models the statistical relationships and correlations between variables. It quantifies the connection between a dependent variable like stock price and various explanatory indicator variables. Linear regression is used to model linear relationships and find the slope and intercept coefficients.
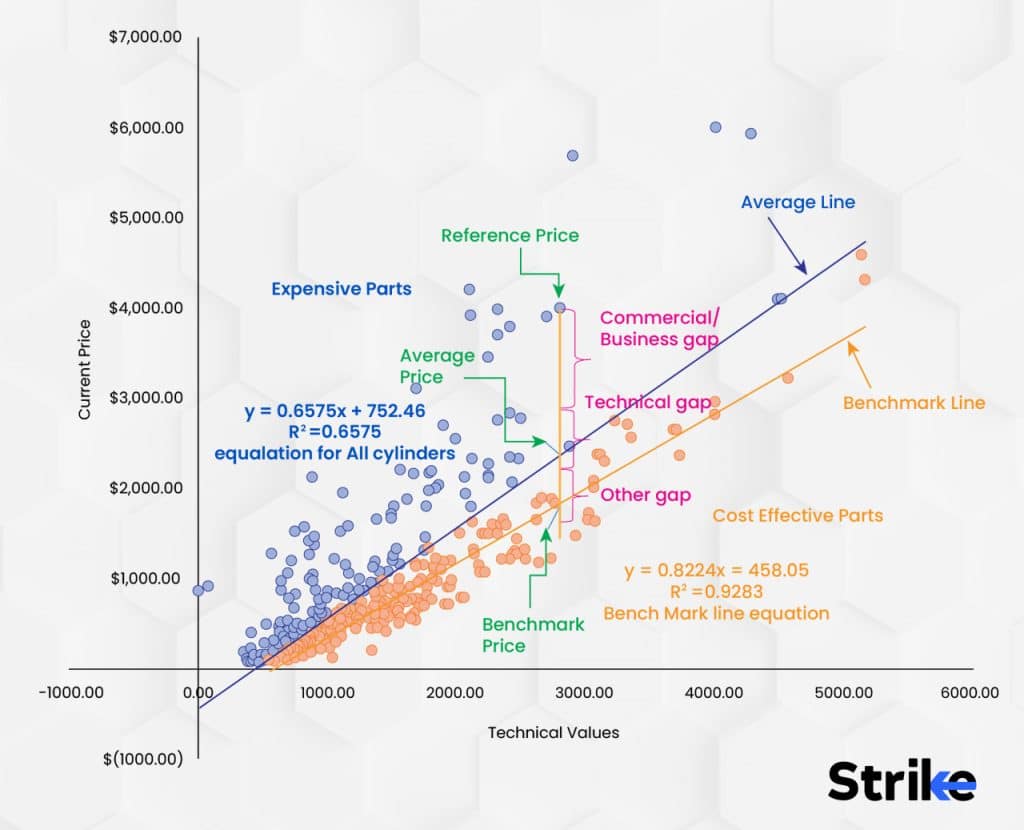
Multiple regression incorporates multiple predictive variables to forecast a stock price or return. Logistic regression handles binary dependent variables like buy/sell signals or over/under events. Polynomial regression fits non-linear curvilinear data relationships. Overall, regression analysis enables analysts to quantify predictive relationships within stock data and build models for forecasting, trading signals, and predictive analytics.
Time Series Analysis
Time series analysis techniques are used to model sequential, time-dependent data like historical stock prices. Auto-regressive integrated moving average (ARIMA) models are designed for forecasting future price trends and seasonality based on lags of prior prices and error terms.
Generalized autoregressive conditional heteroskedasticity (GARCH) models the way volatility and variance of returns evolve over time. Exponential smoothing applies weighted moving averages to historical data to generate smoothed forecasts. Time series analysis produces statistically-driven models for predicting future stock prices and volatility.
Hypothesis Testing
Statistical hypothesis testing evaluates assumptions and theories about relationships and predictive patterns within stock market data. T-tests assess whether the means of two groups or samples are statistically different.
Analysis of variance (ANOVA) compares the means of multiple groups, widely used in evaluating predictive variables for algorithmic trading systems. Chi-squared tests determine relationships between categorical variables like price direction classifications. Hypothesis testing provides the statistical framework for quantifying the probability of data-driven ideas about markets.
Combining statistical modeling competency with programming skills allows financial quants to gain an informational edge from market data. The wide array of statistical techniques available provide mathematically-grounded rigor for unlocking stock market insights.
What Are the Types of Statistical Analysis?
There are five main types of statistical analysis. Below is a details description of the five.
Descriptive Statistics
Descriptive statistics provide simple quantitative summaries about the characteristics and patterns within a collected data sample. This basic statistical analysis gives a foundational overview of the data before applying more complex techniques. Measures of central tendency including the mean, median, and mode calculate the central values that represent the data. Measures of dispersion like the range, variance, and standard deviation quantify the spread and variability of data. Graphical representations such as charts, histograms, and scatter plots visualize data distributions. Frequency distributions through quartiles and percentiles show the proportion of data values within defined intervals. Correlation analysis calculates correlation coefficients to measure the statistical relationships and covariation between variables. Descriptive statistics help analysts explore, organize, and present the core features of a data sample.
Inferential Statistics
Inferential statistics allow analysts to make estimates and draw conclusions about a wider total population based on a sample. Statistical inference techniques include estimation methods to approximate unknown population parameters like mean or variance using sample data inputs. Hypothesis testing provides the framework for statistically accepting or rejecting claims based on p-values and significance levels. Analysis of variance (ANOVA) compares differences in group means. Overall significance testing quantifies the statistical significance of results and relationships uncovered in sample data analysis. Inferential statistics apply probability theory to generalize findings from samples to larger populations.
Predictive Analytics
Predictive analytics leverages statistical modeling techniques to uncover patterns within data that can be used to forecast future outcomes and events. Regression analysis models linear and nonlinear relationships between variables that can generate predictive estimates. Time series forecasting approaches like ARIMA and exponential smoothing model historical sequential data to predict future points. Classification models including logistic regression and decision trees categorize cases into groups that are used for predictive purposes. Machine learning algorithms uncover hidden data patterns to make data-driven predictions. Predictive analytics provides statistically-driven models for forecasting.
Multivariate Analysis
Multivariate analysis studies the interactions and dependencies between multiple variables simultaneously. This reveals more complex statistical relationships. Factor analysis reduces a large set of correlating variables into a smaller number of underlying factors or principal components. Cluster analysis groups data points with similar properties into categories. Conjoint analysis quantifies consumer preferences for certain feature combinations and levels. MANOVA (multivariate analysis of variance) compares multivariate group differences based on multiple dependent variables.
Quantitative Research
Many fields apply statistical analysis to quantitative research that uses empirical data to uncover insights, relationships, and probabilities. Medical research leverages statistics in clinical trials, epidemiology, and public health studies. Social sciences use surveys, econometrics, and sociometrics to model human behaviors and societies. Businesses apply statistics to marketing analytics, financial modeling, operations research, and data science. Data analytics fields employ statistical learning theory and data mining algorithms to extract information from big data. Across industries, statistics bring data-driven rigor to modeling real-world scenarios and optimization.
A diverse toolkit of statistical methodologies is available to address different analytical needs and situations. Selecting the proper techniques allows organizations to transform raw data into actionable, statistically-valid insights that enhance strategic decision-making.
Can Statistical Analysis Help Predict Stock Market Trends and Patterns?
Yes, Statistical analysis is an important tool that provides valuable insights into the behavior of stock markets. By analyzing historical data using statistical techniques, certain recurring trends and patterns can be identified that may have predictive power.
What are the Advantages of Statistical Analysis for Stock Market?
Statistical analysis is a very useful tool for analyzing and predicting trends in the stock market. Here are 12 key advantages of using statistical analysis for stock market investing.
1. Identify Trends and Patterns
Statistical analysis allows investors to identify historical trends and patterns in stock prices and market movements. By analyzing price charts and financial data, statistics reveal recurring patterns that signify underlying forces and dynamics. This helps investors recognize important trend shifts to capitalize on or avoid.
2. Quantify Risks
Statistical measures like volatility and beta quantify the risks associated with individual stocks and the overall market. This allows investors to make more informed decisions on position sizing, portfolio allocation, and risk management strategies. Statistical analysis provides objective measures of risk instead of relying on guesswork.
3. Test Investment Strategies
Investors use statistical analysis to backtest investment strategies. By analyzing historical data, investors evaluate how a given strategy would have performed in the past. This provides an objective way to compare strategies and determine which have the highest risk-adjusted returns. Statistical significance testing determine if performance differences between strategies are meaningful or simply due to chance.
4. Optimize Portfolios
Advanced statistical techniques allow investors to optimize portfolios for characteristics like maximum returns given a level of risk. Statistical analysis also optimize weights between asset classes and smooth portfolio volatility through correlational analysis between assets. This leads to strategically constructed, diversified portfolios.
5. Valuate Stocks
Many valuation models rely on statistical analysis to determine the intrinsic value of a stock. Discounted cash flow models, dividend discount models, and free cash flow models all incorporate statistical analysis. This provides an objective basis for determining if a stock is over or undervalued compared to statistical estimates of fair value.
6. Predict Price Movements
Some advanced statistical methods are used to predict future stock price movements based on historical prices and trends. Methods like regression analysis, ARIMA models, and machine learning algorithms analyze data to make probability-based forecasts of where prices are headed. This allows investors to make informed trading decisions.
7. Understand Market Sentiment
Measurements of market sentiment derived from statistical analysis of survey data, volatility, put/call ratios, and other sources help quantify the overall mood of investors. This reveals valuable insights about market psychology and where the market is headed next.
8. Gauge Earnings Surprises
Statistics measure the tendency of a stock to beat, meet, or fall short of earnings expectations. Investors use this to predict earnings surprise potential and make more profitable trades around quarterly earnings announcements.
9. Assess Economic Indicators
Key economic indicators are tracked and analyzed statistically to gauge economic health. Investors leverage this analysis to understand how overall economic conditions impact different stocks and sectors. This allows more informed investing aligned with macroeconomic trends.
10. Quantify News Impacts
Statistical methods allow analysts to objectively quantify and model the impacts of news events on stock prices. This identifies how strongly different types of news historically affect a stock. Investors then better predict price reactions to corporate events and news.
11. Control for Biases and Emotions
Statistics provide objective, probability-based estimates that remove subjective biases and emotional reactions from investing. This gives investors greater discipline and logic in their analysis versus making decisions based on gut feelings.
12. Enhance Overall Decision Making
The probability estimates, risk metrics, predictive modeling, and other outputs from statistical analysis give investors an information edge. This allows them to make more rational, data-driven decisions boosting overall investing success. Statistics enhance processes from stock selection to risk management.
Statistical analysis empowers investors with a quantitative, objective approach to dissecting mountains of data. This leads to superior insights for finding opportunities, gauging risks, constructing strategic portfolios, predicting movements, and ultimately making more profitable investment decisions. The above 12 advantages demonstrate the immense value statistical techniques provide for stock market analysis.
What Are the Disadvantages of Using Statistical Analysis in The Stock Market?
Below are 9 key disadvantages or limitations to using statistics for stock market analysis:
1. Past Performance Doesn’t Guarantee Future Results
One major limitation of statistical analysis is that past performance does not guarantee future results. Just because a stock price or trend behaved a certain way historically does not mean it will continue to do so in the future. Market dynamics change over time.
2. Data Mining and Overfitting
When analyzing huge datasets, it is possible to data mine and find spurious patterns or correlations that are not statistically significant. Models are sometimes overfit to historical data, failing when applied to new data. Validity and statistical significance testing is needed to avoid this.
3. Change is Constant in Markets
Financial markets are dynamic adaptive systems characterized by constant change. New technologies, market entrants, economic conditions, and regulations all impact markets. So statistical analysis based on historical data misjudge future market behavior.
4. Analyst and Model Biases
Every statistical analyst and model approach inevitably has some biases built in. This sometimes leads to certain assumptions, variables, or data being under/overweighted. Models should be continually reevaluated to check if biases affect outputs.
5. False Precision and Overconfidence
Statistical analysis fosters false confidence and an illusion of precision in probability estimates. In reality, markets have a high degree of randomness and probability estimates have errors. Caution is required when acting on statistical outputs.
6. Data Errors and Omissions
Real-world data contain measurement errors, omissions, anomalies, and incomplete information. This “noise” gets incorporated into analysis, reducing the reliability of results. Data cleaning and validation processes are critical.
7. Correlation Does Not Imply Causation
Correlation between variables does not prove causation. Though related statistically, two market factors does not have a cause-and-effect relationship. Understanding fundamental drivers is key to avoid drawing false causal conclusions.
8. Insufficient Data
Rare market events and new types of data have insufficient historical data for robust statistical analysis. Outputs for new stocks or indicators with minimal data are less reliable and have wide confidence intervals.
9. Fails to Incorporate Qualitative Factors
Statistics analyze quantitative data but markets are also driven by qualitative human factors like investor psychology, management decisions, politics, and breaking news. A statistics-only approach misses these nuances critical for investment decisions.
To mitigate the above issues, experts emphasize balancing statistical analysis with traditional fundamental analysis techniques and human oversight. Key practices when using statistics for stock market analysis include:
Statistical analysis is an incredibly useful tool for stock market investors if applied properly. However, its limitations like data errors, biases, and the inability to incorporate qualitative factors must be acknowledged. Blind faith in statistics alone is dangerous. But combined with robust validation procedures, fundamental analysis, and human discretion, statistics enhance investment decisions without leading to overconfidence. A balanced approach recognizes the advantages statistics offers while mitigating the potential downsides.
What Role Does Statistical Analysis in Risk Management and Portfolio Optimization?
Statistical analysis plays a pivotal role in effective risk management and portfolio optimization for investors. Key ways statistics are applied include quantifying investment risk, determining optimal asset allocation, reducing risk through diversification, and stress testing portfolios.
Statistical measures like standard deviation, value at risk (VaR), and beta are used to quantify investment risk. Standard deviation shows how much an investment’s returns vary from its average. It indicates volatility and total risk. VaR analyzes historic returns to estimate the maximum loss expected over a period at a confidence level. Beta measures market risk relative to broader indexes like the S&P 500. These statistics allow investors to make “apples to apples” comparisons of total risk across different securities.
Asset allocation involves determining optimal percentages or weights of different asset classes in a portfolio. Statistical techniques analyze the risk, return, and correlations between asset classes. Assets with lower correlations provide greater diversification. Analyzing historical returns and standard deviations enables optimization of asset weights for a desired portfolio risk-return profile.
For example, Alice wants high returns with moderate risk. Statistical analysis shows stocks earn higher returns than bonds historically but have higher volatility. By allocating 60% to stocks and 40% to bonds, Alice maximizes returns for her target risk tolerance based on historical data.
Diversification involves allocating funds across varied assets and securities. Statistical analysis quantifies how the price movements of securities correlate based on historical data. Assets with lower correlations provide greater diversification benefits.
By statistically analyzing correlations, investors can construct diversified portfolios that smooth out volatility. For example, adding foreign stocks to a portfolio of domestic stocks reduces risk because daily price movements in the two assets are not perfectly correlated. Statistical analysis enables calculating optimal blends for diversification.
Stress testing evaluates how portfolios would perform under adverse hypothetical scenarios like recessions. Statistical techniques including Value-at-Risk analysis, Monte Carlo simulations, and sensitivity analysis are used.
For example, a Monte Carlo simulation randomly generates thousands of what-if scenarios based on historical data. This reveals the range of potential gains and losses. Investors can then proactively alter allocations to improve resilience if statistical stress tests show excessive downside risks.
Below are the key advantages of using statistical analysis for risk management and portfolio optimization.
- Provides objective, quantitative measurements of risk instead of subjective qualitative judgments. This means that the system uses data and statistics to measure risk, rather than relying on human judgment.
- Allows backtesting to evaluate how different asset allocations would have performed historically, based on actual data. This means that the system is used to test different investment strategies against historical data to see how they would have performed.
- Can analyze a wider range of potential scenarios through simulations than human anticipation alone. This means that the system can consider a wider range of possible outcomes than a human could.
- Considers not just individual asset risks but also important correlations between asset classes. This means that the system can take into account how different assets are correlated with each other, which can help to reduce risk.
- Enables continuous monitoring and backtesting to update statistics as markets change. This means that the system is used to track and update investment strategies as the market changes.
- Allows customizing portfolio construction to individual risk tolerances using historical risk-return data. This means that the system is used to create portfolios that are tailored to individual risk tolerances.
- Provides precision in allocating weights between classes to fine-tune a portfolio’s characteristics. This means that the system is used to allocate assets in a precise way to achieve specific investment goals.
- Empowers investors to maximize returns for a defined level of risk. This means that the system can help investors to achieve the highest possible returns for a given level of risk.
Experienced human judgment is also essential to account for qualitative factors not captured by historical statistics alone. Used responsibly, statistical analysis allows investing risk to be minimized without sacrificing returns.
How Can Statistical Analysis Be Used to Identify Market Anomalies and Trading Opportunities?
Statistics reveal mispricings and inefficiencies in the market. The key statistical approaches used include correlation analysis, regression modeling, and machine learning algorithms.
Correlation analysis measures how strongly the prices of two securities move in relation to each other. Highly correlated stocks tend to move in tandem, while low correlation means the stocks move independently. By analyzing correlations, investors can identify peers of stocks, industries tied to economic cycles, and diversification opportunities.
For example, an automotive stock will be highly correlated with other auto stocks but less correlated to food companies. Identifying correlations allows capitalizing when an entire correlated industry is mispriced. It also prevents overexposure by diversifying across stocks with low correlation.
Regression modeling finds statistical relationships between independent predictor variables and a dependent target variable. In finance, regression can predict stock price movements based on factors like earnings, economic growth, and commodity prices that tended to coincide historically.
Current data suggests a stock is mispriced relative to what regression models forecast, and a trading opportunity exists. For example, regression shows rising oil prices predict gains for energy stocks. If oil is rallying but energy stocks lag, the model indicates they are anomalously underpriced.
Machine learning algorithms discover subtle patterns in huge datasets. By analyzing technical indicators and prices, algorithms like neural networks model price action to forecast movements. When new data deviates from algorithmic price predictions, it flags an anomaly.
Statistical analysis allows investors to take an evidence-based approach to identifying actionable market inefficiencies. By quantifying relationships between myriad variables, statistics reveal securities where current prices diverge from fair value or model-predicted values. Combining these analytical techniques with human judgment enables investors to consistently exploit mispriced assets for excess returns.
How to Analyse Stocks?
Statistical analysis is a powerful tool for stock market investors. Follow these key steps to incorporate statistical analysis into stock research.
1. Gather Historical Price Data
Compile historical daily closing prices for the stock going back multiple years. The longer the price history, the better. Source clean data without gaps or errors which could distort analysis.
2. Calculate Returns
Convert closing prices into a time series of daily, weekly, or monthly returns. Percentage returns offer more analytical insight than just prices. Calculate returns by dividing today’s price by yesterday’s price and subtracting 1.
3. Graph Price History
Visually review price charts over different timeframes. Look for periods of volatility or unusual price spikes that could skew statistical assumptions of normality. Check for any structural breaks in longer term trends.
4. Measure Central Tendency
Measure central tendency to identify the average or typical return over your sample period. Mean, median, and mode offer three statistical measures of central tendency. The median minimizes the impact of outliers.
5. Quantify Variability
Use statistical dispersion measures like variance, standard deviation, and coefficient of variation to quantify return variability and risk. Compare volatility across stocks to make “apples to apples” risk assessments.
6. Analyze Distributions
Evaluate the shape of return distributions. Use histograms, skewness, and kurtosis metrics to check normality assumptions. Non-normal distributions like fat tails indicate higher probabilities of extreme returns.
7. Run Correlations
Correlation analysis measures if returns tend to move together or independently between two stocks. High correlations mean stocks offer less diversification benefits when combined.
8. Build Regression Models
Use regression analysis to model relationships between stock returns and explanatory variables like market returns, interest rates, earnings, etc. This reveals drivers of returns.
9. Forecast with Time Series Models
Time series models like ARIMA apply statistical techniques to model stock price patterns over time. This enables forecasting near-term returns based on historical trends and seasonality.
Incorporating statistical analysis like returns, risk metrics, forecast modelling, backtesting, and Monte Carlo simulations significantly improves stock analysis and predictions. Combining statistical techniques with traditional fundamental analysis provides a probabilistic, quantitatively-driven approach to evaluating investment opportunities and risks. However, statistics should supplement human judgment, not replace it entirely. No model captures all the nuances that drive markets. But used prudently, statistical tools enhance analytical precision, objectivity, and insight when researching stocks.
Can Statistical Analysis Predict the Stock Market?
Yes, the potential for statistical analysis to forecast stock market movements has long intrigued investors. But while statistics can provide insights into market behavior, the ability to reliably predict future prices remains elusive. On the surface, the stock market would seem highly predictable using statistics. Securities prices are simply data that is quantified and modeled based on historical trends and relationships with economic factors. Sophisticated algorithms detect subtle patterns within massive datasets. In practice however, several challenges confront statistical prediction of markets:
When predictive statistical models for markets become widely known, they get arbitraged away as investors trade to profit from the forecasted opportunities. Widespread knowledge of even a valid exploitable pattern may cause its demise. Predictive successes in markets tend to be short-lived due to self-defeating effects.
Is Statistical Analysis Used in Different Types of Markets?
Yes, statistical analysis is used across different market types. Statistical analysis is widely used in stock markets. Techniques like regression modeling and time series analysis help predict stock price movements based on historical trends and relationships with economic variables. Metrics like volatility and beta quantify risk and correlation.
Is Statistical Analysis Used to Analyse Demand and Supply?
Statistical analysis is a valuable tool for modeling and forecasting demand and supply dynamics. By quantifying historical relationships between demand, supply, and influencing factors, statistics provide data-driven insights into likely market equilibrium points.
Statistics are used to estimate demand curves showing quantity demanded at different price points. Regression analysis determines how strongly demand responds to price changes based on historical data. This price elasticity of demand is quantified by the slope of the demand curve.
Statistics also reveal drivers of demand beyond just price. Multiple regression models estimate demand based on income levels, population demographics, consumer preferences, prices of related goods, advertising, seasonality, and other demand drivers. Understanding these relationships through statistical modeling improves demand forecasts.
Statistical techniques play a pivotal role in understanding the dynamics of demand and supply zones in market analysis. They are particularly adept at modeling supply curves, which depict the quantity suppliers are willing to produce at various price points. This is achieved through regression analysis, quantifying the price elasticity of supply by examining historical production volumes and prices. This approach helps in identifying supply zones – regions where suppliers are more likely to increase production based on pricing.
Similarly, the demand side can be analyzed through these statistical methods. Factors like consumer preferences, income levels, and market trends are evaluated to understand demand zones – areas where consumer demand peaks at certain price levels.
Moreover, other elements affecting the supply are statistically assessed, including input costs, technological advancements, regulations, the number of competitors, industry capacity, and commodity spot prices. Each of these can significantly influence production costs and, consequently, the supply.
Multiple regression models are employed to statistically determine the impact of each driver on the supply, aiding in the precise delineation of supply zones. This comprehensive statistical evaluation is vital in mapping out demand and supply zones, crucial for strategic decision-making in business and economics.

![85 Common Stock Market Terminologies for Dummies [Updated List for 2025] 64 85 Common Stock Market Terminologies for Dummies [Updated List for 2025]](https://www.strike.money/wp-content/uploads/2025/04/Popular-Stock-Market-Terms-for-Beginners-Banner.png)







No Comments Yet.