Vomma in Option Trading: Definition, Functionality, Advantages, and Limitations

• Strike
• Options Trading Guide
• Vomma in Option Trading: Def...

Vomma is a Greek metric used in options trading that measures the rate of change of vega in relation to volatility. Vomma specifically quantifies the second order sensitivity of an option’s value to a 1% change in volatility. Mathematically, it is the first partial derivative of vega with respect to volatility. The higher the absolute vomma value, the greater the impact even small volatility changes have on the vega of the option.

Vomma has useful applications in options trading strategies and analysis. It helps gauge exposure to fast moving implied volatility. Higher vomma signals higher risk if volatility starts swinging rapidly. Strategies like iron condors with offsetting long and short options have minimal vomma, reducing risks from volatility changes. Vomma identifies mispriced options based on abnormal volatility term structures. Comparing vomma across different strikes highlights anomalies. Portfolio vomma indicates overall volatility risk. Traders adjust position sizing or hedge vega risk if total vomma is high.

What is Vomma in Options?

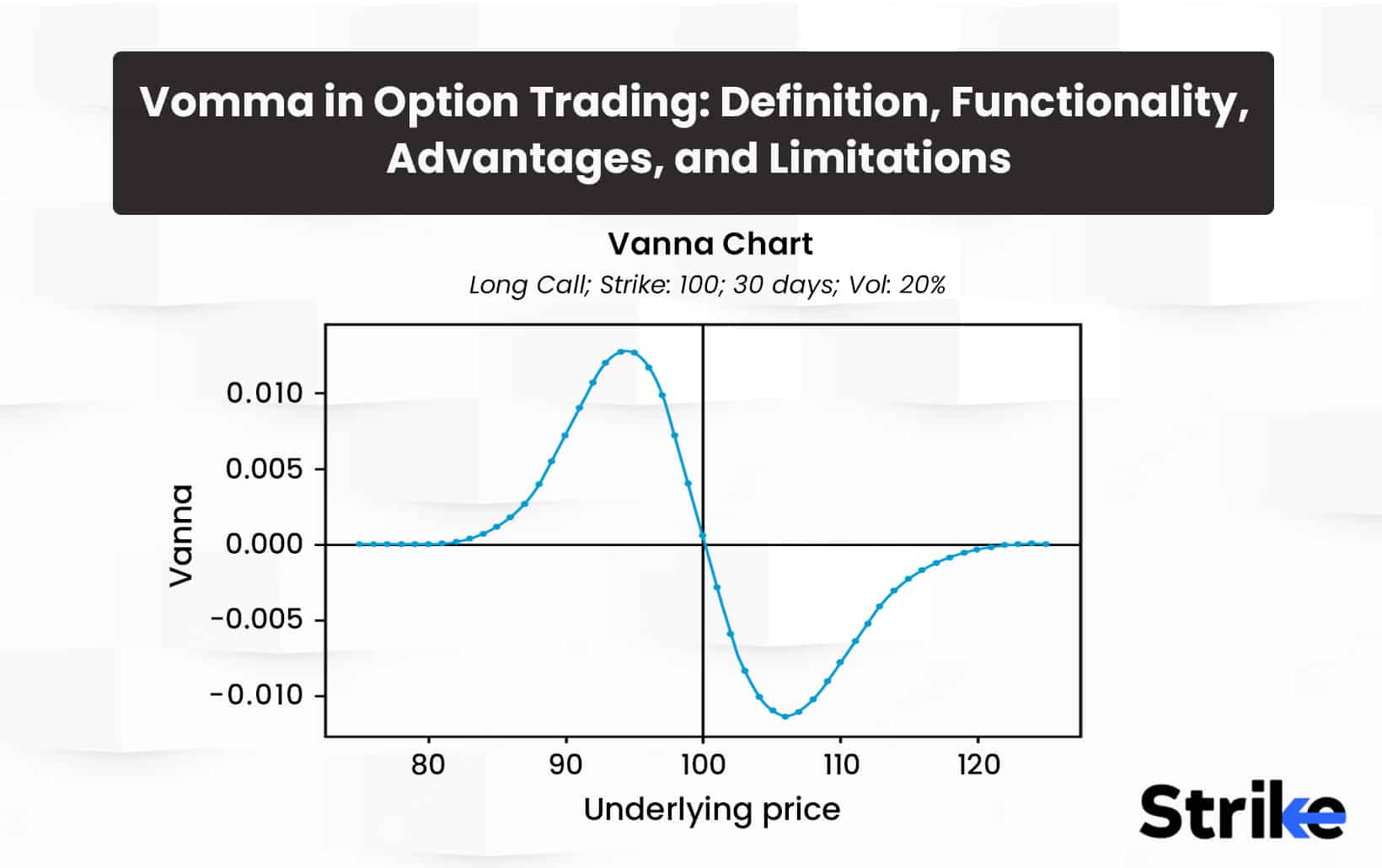
Vomma in options measures the rate of change in an option’s vega with respect to changes in the underlying asset’s volatility. Vega measures an option’s sensitivity to changes in volatility, while vomma measures the sensitivity of vega itself to volatility. 

Vomma is the second partial derivative of the option pricing model with respect to volatility. The calculation is provided below for a European call option.

Vomma indicates the convexity of the option’s value relative to volatility. A positive vomma means the option’s vega increases as volatility rises. This indicates the option has a convex payoff structure in relation to volatility. A negative vomma means vega decreases as volatility rises, indicating a concave payoff profile.

Vomma arises because vega is not linear in relation to volatility. Vega increases slowly as volatility rises from low volatility levels. But vega increases rapidly with rising volatility at higher volatility levels. This convex shape means vomma is positive.

Vomma is typically small for at-the-money options, and increases for deep-in-the-money and deep out-of-the-money options. This is because atm options have near-linear vega profiles, while itm and otm options display greater convexity in vega.

Traders use vomma to gauge how sensitive an option’s vega is across different volatility levels. Vomma is used to create volatility spreads that profit from diverging volatility sensitivities between two or more options. 

Strategies involving vomma aim to exploit the convexity in options prices. For example, a positive vomma means long volatility positions benefit from upward volatility spikes more than they suffer from muted declines in volatility.

Vomma is positive for most options, due to the convex shape relating volatility to option prices. Vomma increases for deep itm and otm options. Atm options have near zero vomma. Vomma is generally highest when volatility is low, and declines as volatility rises.

Vomma is used to create spread positions that benefit from vega divergence between two options. Vomma adds a “volatility of volatility” dimension for traders managing volatility risk. Vomma is valuable for structuring positions that have asymmetric payoff profiles depending on future volatility.

Long volatility positions gain from upward volatility spikes more than they lose from muted declines with positive vomma. This asymmetric payoff profile is profitable if volatility trends higher over time.Vomma trading involves positioning long and short volatility exposures across different vomma profiles. This aims to benefit from differing sensitivities to volatility  changes.

Portfolios are structured to have positive vomma on average. This makes the portfolio vega increase if future realised volatility exceeds current implied volatility. Negative vomma positions are used as volatility-stabilising hedges. These offset some losses during volatility spikes. Vomma spread positions profit from relative value trades between mispriced options based on vomma divergences.

Why is Vomma important in Option Trading?

Vomma plays an important role in options trading by quantifying the nonlinearity in vega across different volatility levels. Vega measures sensitivity to volatility, while vomma measures the sensitivity of vega itself. This second-order effect is crucial for managing volatility risk and structuring positions with asymmetric volatility exposures. Vomma is crucial for option traders for a number of reasons.

Vomma measures the convexity of an option’s value relative to volatility due to the nonlinear relationship between volatility and option prices. Vomma allows traders to quantify this nonlinearity and assess how pronounced the convexity profile is.

Positive vomma means volatility spikes have an outsized impact compared to low volatility periods. This asymmetry is beneficial for volatility-dependent strategies. Vomma allows constructing asymmetric exposures not captured by static vega alone.

Vomma provides a more complete picture of volatility risk. Portfolios are structured to have positive vomma on average to benefit from upward volatility spikes. Vomma-based hedging helps mitigate losses during periods of falling volatility. 

Vomma allows trading the volatility of volatility itself. Volatility swaps, futures and options with different vomma profiles are traded to capitalise on volatility level changes. This adds a new volatility trading dimension beyond just vega.

Higher vomma indicates vega changes more rapidly across volatility levels. Lower vomma means vega is more stable despite volatility changes. Vomma informs traders on the steadiness of vega exposure.

Vomma divergences between options reveals mispriced volatility exposures. This creates volatility arbitrage and relative value trades based on vomma dispersion.

Vomma varies across option expirations, reflecting differences in volatility term structures. Vomma analysis provides insight into how volatility sensitivity changes across the term structure.

Vomma changes with moneyness, capturing the volatility skew embedded in option prices. Vomma quantifies how volatility exposure differs across strike prices.

Vomma metrics help identify attractive ratio spreads and dispersion trades between volatilities. Vomma divergences signal opportunities for volatility pairs trading.

Many trading strategies have indirect volatility exposure through convexity. Analysing vomma improves hedging of these complex exposures.

How does Vomma differ from other option Greeks?

Vomma is differ from other options greeks because Vomma measures the rate of change of an option’s vega with respect to volatility.

Vomma is a second-order Greek, measuring the sensitivity of vega rather than just the price itself. Other Greeks like delta, gamma and theta are first-order derivatives measuring the sensitivity of the option price.

Vomma captures the volatility of implied volatility. It quantifies how vega changes across different volatility levels. Other Greeks focus on directional exposure to primary risk factors like spot prices, time decay or interest rates.

Vomma indicates the convexity of an option payoff profile relative to volatility. Positive vomma signifies increasing vega at higher volatility levels. Other Greeks have a linear relationship to the underlying risk factor.

Vomma creates asymmetric exposure to volatility spikes over low volatility environments. This distinct payoff profile benefits from upward volatility trends. Other Greeks create symmetric risk exposures.

Vomma is considered a secondary Greek compared to primary Greeks like delta and vega as a second-order sensitivity. Primary Greeks give the most direct risk sensitivities.

omma captures the volatility skew between strike prices and expiration dates. Other Greeks only quantify skew indirectly through the option price.

Vomma is important for properly hedging vega exposure given how vega changes across volatility levels. Other Greeks hedge linear exposures.

Vomma allows capitalising on differences in volatility curvature between options. Other Greeks identify mispricings in the level of implied volatility.

Vomma approximates the convexity exposure similar to a long variance swap. Other Greeks do not mimic variance swap payouts.

Moreover, Vomma measures how stable Vega is across changing volatility environments. Other Greeks assume static exposures. 

How does Vomma work?

Vomma works as a measurement of how an option’s delta changes as volatility changes. It quantifies how rapidly vega changes as volatility fluctuates. Vomma indicates the curvature and convexity in the relationship between volatility and option prices.

Vomma is calculated as the second partial derivative of the option price with respect to volatility. The formula for a European call option is below.

Vomma = ∂2V/∂σ2 

Where V is the option value, and σ is the volatility. This measures the rate of change of vega as volatility changes.

Vega is not linear across different volatility levels. Vega increases slowly as volatility rises at low volatility and at higher volatility, vega accelerates higher. This convex profile means vomma is positive for most options.

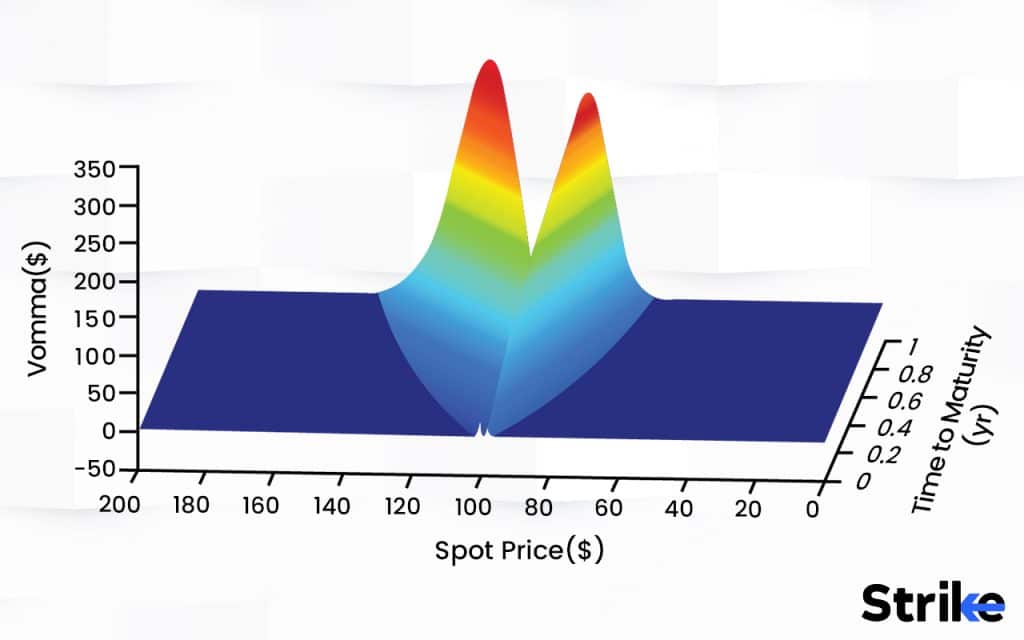
Vomma increases for deep in-the-money and out-of-the-money options. Near-the-money options have near zero vomma. Itm and otm options display greater convexity between volatility and option value. Vomma is highest when volatility levels are low, and declines as volatility rises. The convexity in vega is most pronounced at lower volatility levels.

Positive vomma creates asymmetric volatility exposure. The position benefits more from upward volatility spikes than it loses from low volatility environments. This payoff asymmetry is attractive if volatility trends higher over time. Higher vomma indicates vega changes more rapidly across different volatility levels. Lower vomma means vega is more stable despite volatility fluctuations.

Vomma allows trading volatility by exploiting differences in vomma between options. Volatility curve trades, dispersion strategies and volatility pairs trades utilise vomma divergences.

Portfolios are structured to have positive vomma on average. This dynamic vega exposure causes the portfolio to benefit from rising volatility. Vomma improves hedging of vega exposure across changing volatility regimes.  Positive vomma creates a convex payoff profile similar to being long a variance swap contract. The position accrues greater positive vega just like a variance swap as volatility rises.

How does Vomma contribute to the sensitivity of options to changes in implied volatility?

Vomma directly measures the sensitivity of an option’s vega to the level of implied volatility. Vega quantifies sensitivity to volatility changes, while vomma gauges the rate of change in vega across different volatility regimes. This secondary order contribution reflects the nonlinear relationship between volatility and option prices.

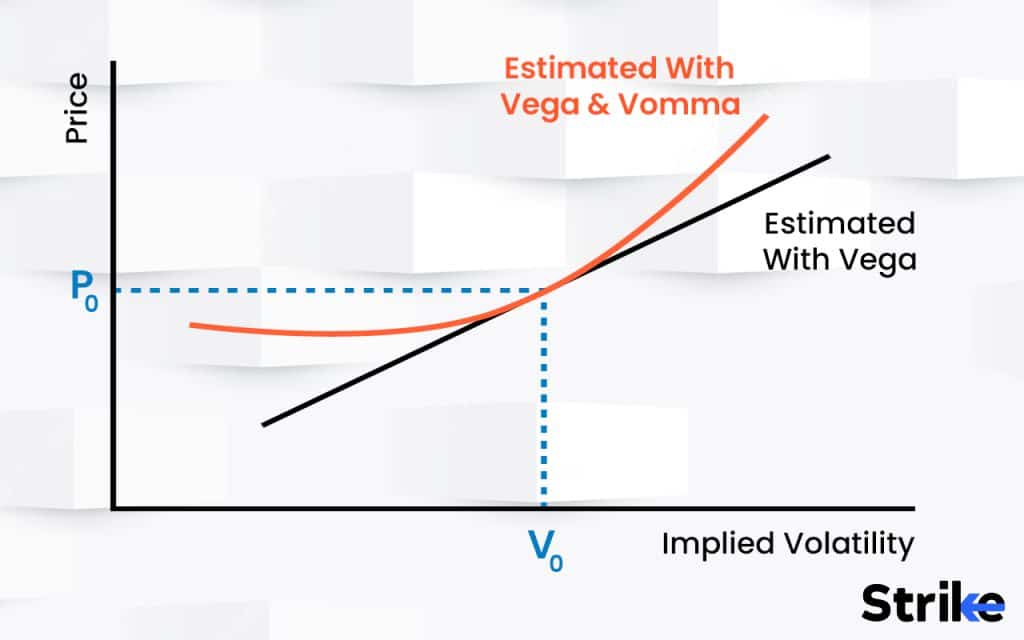
The convexity of vega means it increases at an accelerating rate as volatility rises. Vomma quantifies this nonlinearity in the vega profile. Positive vomma indicates convexity, with vega becoming more sensitive at higher volatility levels. Vomma determines how rapidly vega changes for a given change in volatility. Higher vomma means vega undergoes larger proportional changes for volatility fluctuations. Lower vomma indicates more subdued vega changes.

Vomma measures the stability of vega across changing volatility environments. Lower vomma signifies vega is steadier despite volatility shifts. Higher vomma indicates unstable vega with greater oscillations. Positive vomma creates asymmetric volatility exposure, with vega spiking dramatically during volatility rallies. This benefits from upward volatility trends. Negative or low vomma contributes to a more symmetric volatility response.

Analysing vomma improves quantification of volatility risk. Portfolio vomma is optimised to benefit from vega rising in volatile markets. Vomma helps structure asymmetric volatility exposures. The nonlinearity in vega makes vomma crucial for properly hedging vega. Hedging based on vomma is more robust across diverse volatility regimes. Low vomma hedges offset high vomma volatility sensitivity. Vomma allows expressing views on volatility itself. Positioning long and short vomma trades volatility level changes and volatility skew shifts.

Vomma divergences identify cheap and rich volatility exposures to exploit in volatility arbitrage strategies. Vomma is key for assessing relative value of volatility instruments. Vomma changes across the volatility term structure, reflecting differences in vega profiles. Vomma indicates how vega sensitivity evolves for different expirations.

What is the formula for calculating Vomma?

The formula for vomma is the second partial derivative of the option price with respect to volatility. The Vomma formula is appropriate for a European call option.

Vomma = ∂2V/∂σ2

Where:

V = Option price 

σ = Volatility

∂2V/∂σ2 = Second partial derivative of option price V with respect to volatility σ

This measures the rate of change of vega with respect to changes in volatility. 

In practice, vomma is estimated numerically using the Black-Scholes option pricing model and calculating small differences even though the formula above defines vomma technically.

This numerical estimation quantifies the rate of change of vega by examining vega values above and below current volatility.

Vomma is determined explicitly using the formula under the Black-Scholes model.

Vomma = Vega x [1 – d1 x stddev(price)] / [stddev(price) x strike price]

Where:

Vega = Options vega sensitivity 

d1 = Black-Scholes d1 standardised price measure

stddev(price) = Annualised standard deviation of underlying price 

Strike Price = Option strike price

This calculates vomma based on the vega amount adjusted for the moneyness of the option.

How does Vomma impact options and their pricing dynamics?

Vomma impacts options and their pricing dynamics by influencing how responsive the option’s delta will be to changes in the underlying’s implied volatility.  Higher vomma means volatility changes will drive greater proportional changes in the option’s price. The price becomes more responsive to volatility shifts. Lower vomma dampens the price impact of changing volatility.

Positive vomma creates asymmetry in how option prices respond to volatility. Prices spike dramatically with volatility surges but decline more modestly amid falling volatility. This asymmetric profile benefits from upward volatility trends.

Vomma indicates the stability of vega across different volatility regimes. Lower vomma means more stable vega and more predictable option price response. Higher vomma causes unstable vega and price response.

Analysing vomma allows better quantification of volatility risk embedded in option prices. Portfolio vomma composition is optimised to benefit from upward volatility spikes.

Vomma spreads allow expressing views on future volatility of volatility. Positioning long vs short vomma aims to profit from changing volatility regimes.

Vomma divergences identify cheap and rich volatility exposures to exploit in volatility arbitrage trades. Vomma is key to assessing relative value.

Vomma is derived explicitly, under the Black-Scholes model, based on the vega, option delta, and volatility values. This quantifies the convexity in price response to volatility changes.

Vomma directly impacts the nonlinearity in option price response to changing volatility. It determines the rate of change of vega across volatility regimes. Vomma is crucial for volatility risk management, volatility trading, and identifying mispriced volatility exposures. It reflects the inherent convexity relating option prices to implied volatility.

What are the potential pitfalls and risks involved in trading Vomma options?

The potential fitfalls and risks involved in trading Vomma options include its complexities, vega miscalculation, etc. Below listed are the 15 important risks to understand. 

1. Complex strategies: Vomma-based trades often utilise complex options strategies like ratio spreads, straddles, strangles, and dispersion trades across multiple legs. These advanced structures have many moving parts and require precision implementation.

2. Vega miscalculation: Inaccurate estimation of vega sensitivity undermines vomma trading strategies. Robust vomma analysis relies on having precise vega calculations across changing volatility levels. 

3. Volatility forecasting errors: Strategies betting on vomma divergence require accurate volatility forecasts. Erroneous volatility expectations invalidate the rationale for vomma relative value trades.

4. Hedging challenges: The dynamic nature of vomma exposure complicates precise vega hedging as volatility changes. Adaptive hedging based on updated vomma estimates is essential but difficult to execute.

5. High transaction costs: Frequent rebalancing and trading multiple option legs makes vomma strategies expensive to implement. The accumulation of transaction costs erodes profit potential.

6. Early exercise risk: Vomma trades using American-style options have early exercise risk that is not captured in standard pricing models. This forces early unwinding of vomma positions.

7. Curve fitting risks: Excessive data mining when fitting volatility curves leads to overfit vomma models. This reduces the predictive reliability of the volatility analytics.

8. Numerical estimation errors: Approximating vomma via numerical differentiation of option prices risks introducing quantification errors. Precision in vomma calculations is vital.

9. Liquidity constraints: Trading on vomma often requires using longer dated options that have poor liquidity. The market impact from trading imposes high costs.

10. Margin and collateral: Vomma positions have dynamic margin needs as market volatility fluctuates. Maintaining sufficient collateral to meet margins is essential.

11. Correlation instability: Strategies relying on stable vomma correlations between specific options face correlation breakdowns during market stresses.

12. Gap risk: Sudden volatility gaps cause abrupt mark-to-market losses before vomma-dependent positions are adjusted.

13. Model risk: Vomma calculations rely on pricing models like Black-Scholes that have deficiencies. Model errors lead to inaccurate vomma estimates.

14. Regime change risk: A regime shift quickly invalidates the vomma exposures since vomma varies across different volatility regimes.

15. Curve calibration risk: Fitting the volatility curve requires calibrating to limited liquid option prices. This misrepresents the full vomma surface.

The complex nature of vomma-based strategies necessitates thorough evaluation of implementation risks and robust risk management. Vomma trading requires continuously adapting to evolving volatility dynamics across markets.

What strategies can traders employ to handle Vomma risks?

Strategies traders employ to handle vomma risks involve understanding how vomma exposes their option positions to changes in implied volatility. Below are the seven main strategies to avoid risks. 

1. Diversification: Constructing multi-legged option positions with offsetting vomma profiles aims to diversify volatility curvature risks. Mixing positive and negative vomma combinations reduces concentration risk.

2. Hedging: Deliberately utilising options with negative or zero vomma hedge the vega exposure of high positive vomma positions. This aims to stabilise overall vega sensitivity as volatility changes.

3. Vomma Scaling: Size positions proportional to their vomma contributions such that the portfolio vomma scaling remains aligned with volatility view.

4. Gamma Hedging: Gamma hedging indirectly stabilises vomma since vomma is affected by gamma . Frequent delta rebalancing aims to control gamma profile.

5. Correlation Analysis: Evaluate historical correlations between vomma on different options to assess stability. Avoid excessive reliance on unstable vomma correlations.

6. Model Validation: Compare vomma estimates across different pricing models to diagnose model risk. Model disparities reveal deficiencies estimating vomma.

7. Vega-Adjusted Sizing: Scale position vega contribution based on current vomma so vega remains aligned with volatility outlook at various volatility levels.

Vomma presents risks that need managing through thoughtful strategies adapted to the trader’s volatility outlook. Effective techniques include constructing diversified, hedged positions while accounting for vomma in scaling and rebalancing decisions. Ongoing monitoring of vomma characteristics like stability and relationships across options aids risk control. Traders that comprehend vomma exposures and devise strategies to mitigate undesirable sensitivity to implied volatility fluctuations better navigate complex volatility-dependent trades.

What factors influence Vomma in option trading?

The factors that influence Vomma in option trading includes moneynes, implied volatility, time to expiration, etc. Below are the nine factors explained. 

1. Moneyness: Vomma increases for deep in-the-money and out-of-the-money options. At-the-money options have near zero Vomma. The convexity of vega is more pronounced for itm and otm options.

2. Implied Volatility: Vomma is highest when implied volatility levels are low. Vomma declines as implied volatility rises. Vega convexity is greatest when volatility is low.

3. Time to Expiration: Vomma generally increases as expiration approaches, peaking around 60-90 days to expiration. Further shortening of time to expiration causes Vomma to decline.

4. Delta: Vomma moves inversely to delta, since high delta itm options have near linear vega. Low delta otm options with convex vega profiles exhibit higher Vomma.

5. Gamma: Vomma is directly affected by gamma given gamma measures the rate of change of delta. Higher gamma contributes to larger Vomma values.

6. Rho: Vomma has an inverse relationship to rho, the sensitivity to interest rates. Higher rho reduces Vomma, while lower rho increases Vomma all else equal.

7. Dividends: Pending dividends reduce Vomma since dividends lower option deltas. Deep otm puts have higher Vomma than comparable calls due to put-call parity.

8. Strike Price: Vomma rises as options move further in-the-money or out-of-the-money due to the convexity of vega relative to strike price.

9. Underlying Price Moves: Vomma declines when underlying prices rise for call options, and declines when underlying prices fall for put options, due to changing moneyness.

How does Vomma behave under different market scenarios?

Vomma behaves differently under different market scenarios. Vomma declines across all options as implied volatility increases. This is because vega exhibits greater convexity at lower volatility levels. However, the vesting impact is greater for high Vomma options.

Vomma increases as implied volatility declines. The convexity in vega becomes more pronounced in low volatility environments. Low Vomma options are less affected than high Vomma alternatives.

Vomma of call options declines while Vomma of put options rises in an upward trending market. This is due to the changing moneyness impact on vega convexity as the underlying asset price moves. Vomma of calls increases while Vomma of puts declines for a downward trending market. The moneyness impact is reversed compared to upward markets.

Absent large volatility fluctuations, Vomma is typically steady while underlying prices stay unchanged. But some variance persists due to time decay adjusting moneyness. Vomma of all options declines substantially during volatility spikes. However, the vega exposure of high Vomma options increases materially despite the Vomma reduction.

Vomma rebounds higher as volatility means reverts lower following a volatility spike. Low Vomma options have relatively stable vega exposure while high Vomma options benefit more.

What strategies can be employed when trading Vomma options?

Strategies for trading Vomma options include strategies that involve being long or short vomma. Position options with different strikes and expirations to benefit from changes in the volatility curve skew based on divergences in Vomma between points on the curve.

1. Vomma Dispersion 

Take advantage of differences in implied volatility between related asset classes by trading options with varying Vomma exposures on each asset. 

2. Vega Hedging

Use options with negative or low Vomma to hedge the vega risk of a directional option position exhibiting high positive Vomma.

3. Vomma Scalping

Capture short-term mean reversion in Vomma by quickly trading volatility spikes and crashes using options across moneyness points.

4. Vomma Arbitrage 

Exploit mispricings in volatility exposure between options by identifying cheap and rich Vomma levels relative to fair value.

5. Vomma Diversification

Construct spread positions using options with offsetting Vomma to diversify risks from volatility changes.

6. Vomma Volatility Targeting

Scale the notional vega exposure based on Vomma contributions to target a portfolio level of volatility sensitivity. 

7. Time Decay Trading 

Take advantage of accelerating time decay on high Vomma options by selling volatility on options with short expiration periods.

8. Vomma Risk Premia

Earn the risk premium associated with volatility uncertainty by collecting Vomma from richly priced low Vomma options.

9. Vomma Swaps

Replicate Vomma exposure using liquidly traded volatility products to efficiently gain long or short Vomma.

10. Vomma Futures Spreading

Leg into Vomma exposures by spreading futures across different expiration dates based on the term structure.

The above strategies for Vomma have to be used in the right time with right guidance for best results. 

What are the benefits of trading Vomma options?

The benefits of trading vomma options include taking advantage of the option’s sensitivity to changes in implied volatility. Properly predicting moves in implied volatility allows options traders to profit whether volatility rises or falls. Trading vomma options also provides exposure to volatility that differs from simply being long or short vega. Here are the eight main benefits of trading vomma options. 

1. Manage vega exposure more dynamically: Vomma provides insights into how vega changes across volatility regimes. This allows better adaptation of vega risk as volatility fluctuates.

2. Construct asymmetric volatility trades: Positive Vomma creates asymmetric exposure that benefits from volatility spikes more than declines. This convexity boosts volatility-dependent strategies.

3. Exploit volatility curve anomalies: Divergences in Vomma across the volatility surface signals relative mispricings to exploit.

4. Enhance volatility risk management: Analysing portfolio Vomma aids in quantifying volatility risks and strategically positioning exposures.

5. Trade volatility of volatility: Vomma enables explicitly trading the volatility of volatility itself as an independent risk factor. 

6. Take advantage of mean reversion: High Vomma tends to mean revert faster after volatility shocks compared to low Vomma.

7. Efficiently hedge vega risk: Low Vomma options is used to hedge high Vomma exposures, stabilising overall vega sensitivity.

8. Leverage term structure dynamics: Vomma varies across the volatility term structure, enabling term structure trading strategies.

Trading vomma options allows for sophisticated management of volatility exposure through understanding an option’s sensitivity to changes in implied volatility. Vomma analysis provides important insights that can help construct effective and risk-adjusted trades tied to expectations of future volatility movements. It enables exploiting inefficiencies in both the options pricing and the volatility surface itself.

How do Vomma options provide potential opportunities for traders to capitalise on changes in implied volatility?

Vomma options provide potential opportunities for traders to capitalise on changes in implied volatility through anticipating how it impacts an option’s delta. Analyzing an option’s vomma value allows traders to deduce how sensitive that option’s price will be to shifts in expected market volatility. Below are seven ways for the same.

1. Asymmetric Volatility Exposure

Options with positive Vomma gain from volatility spikes more than they lose from low volatility environments. This asymmetry is beneficial if volatility trends higher over time.

2. Volatility Curve Arbitrage 

Divergences in Vomma across the volatility surface signals relative mispricings to exploit through volatility curve arbitrage strategies.

3. Volatility Skew Trading

Differences in Vomma between options at various strike prices allows benefiting from volatility skew changes.

4. Vega Hedging

Options with negative or minimal Vomma are used to hedge the vega risk of positions with substantial positive Vomma. This stabilises overall volatility exposure.

5. Vomma Scalping

Changes in Vomma create short-term mean reversion trading opportunities around volatility shocks and spikes.

6. Time Decay Trading

The convexity of Vomma enables strategies selling inflated volatility in front of scheduled events and earnings announcements.

7. Volatility Factor Timing

Scaling options exposure proportional to Vomma allows increasing vega when volatility appears cheap and decreasing vega when rich.

Understanding vomma opens up potential opportunities for traders to monetize their views on how implied volatility evolves in the future.

What are the drawbacks of trading Vomma options?

The biggest drawbacks of trading vomma options is that vomma trading often utilises complex multi-leg strategies that are challenging to implement and manage. Below are 13 more such drawbacks, 

1. Liquidity Constraints: Trading far from the money options with the highest Vomma suffer from wide bid-ask spreads and thin liquidity.

2. Numerically Intensive: Precisely calculating Vomma requires intensive numerical estimation that is prone to quantification errors. 

3. Model Risk: Vomma calculations rely on derivative pricing models like Black-Scholes which have inherent limitations.

4. Difficult Hedging: The dynamic nature of Vomma makes static hedging challenging and requires constant adjustment.

5. Unstable Correlations: Relative value trades relying on Vomma correlations face risks if those correlations break down.

6. Regime Change Vulnerability: Shifts between volatility regimes quickly invalidate expected Vomma exposures.

7. Computationally Intensive: Frequent recomputation of Vomma metrics is needed but is computationally demanding.

8. Forecasting Error Risk: Strategies betting on Vomma divergence rely heavily on volatility forecast accuracy.

9. Significant Gamma Risk: Vomma trades often have substantial gamma risk requiring intensive management.

10. Curve Fitting Risk: Excessive data mining when fitting volatility surfaces lead to overfit Vomma models. 

11. Margin and Collateral: Vomma trades typically require dedicating significant margin and collateral.

12. Gap Risk: Sudden volatility gaps create abrupt mark-to-market losses before Vomma positions are adjusted.

13. Crowded Trades: Vomma trading strategies become very crowded, leading to convergent loss risk.

The complexities require extensive risk management, numerical precision, liquidity planning, robust modelling, and adaptation to shifting volatility regimes even though Vomma provides valuable trading signals.

What is the expected return on a Vomma option?

The expected return on a Vomma option depends on the projected future realised volatility over the option’s lifetime relative to currently implied volatility levels.

Positive Vomma options have the potential for enhanced returns if future realised volatility exceeds current implied volatility. This is because positive Vomma creates asymmetric upside exposure to increasing volatility.

Specifically, positive Vomma options benefit from volatility spikes more than they suffer from declines in volatility. This convexity skews returns to the upside if volatility trends higher on average.

For example, a 5 percentage point increase in volatility would boost the option value and enhance returns if an option has a +0.05 Vomma. However, a 5 percentage point drop in volatility would have a more muted impact on value.

The rate of change of vega quantified by positive Vomma provides leveraged upside exposure to rising volatility without symmetric downside exposure.

However, the upside from positive Vomma relies on volatility indeed rising from its current implied levels observed in option prices. Positive Vomma will reduce returns if future realised volatility stays constant or decreases.

The inflated premium paid for positive Vomma options represents a drag on returns in stagnant low volatility environments. Traders pay up for convexity they do not ultimately realise.

Traders must have an accurate forecast of higher future realised volatility compared to current implied volatility priced into options to capitalise on positive Vomma,.

Positive Vomma options are expected to exhibit lower returns compared to similar delta options with near zero Vomma without a volatility term structure tilted in favour of rising volatility,.

How does the expected return on a Vomma option vary based on different market conditions and implied volatility levels?

The expected return on a vomma option varies based on different market conditions and implied volatility levels because The sensitivity of an option’s price to changes in implied volatility, as measured by its vomma, depends significantly on the prevailing level of implied volatility for the underlying asset.

Positive Vomma options have lower expected return when implied volatility is high. The volatility premium is already elevated, limiting further upside. Meanwhile, vega decay drag dominates. Here is a summary of how various market circumstances and implied volatility levels might affect the projected return on a Vomma option.

Low Implied Volatility: Positive Vomma options have greater return potential if volatility trends higher with low implied volatility. The convexity capitalises on an upward volatility shift.

Rising Implied Volatility: Positive Vomma enhances returns as the asymmetric convexity accumulates gains during periods of consistently rising implied volatility,.

Falling Implied Volatility: Positive Vomma options lag when implied volatility is constantly dropping because the vega decay impact reduces performance daily.

Stable Volatility: Positive Vomma options tend to underperform neutral Vomma options as traders overpay for unrealized convexity in range bound low volatility environments .

Volatility Mean Reversion: Vomma return benefits from volatility mean reversion which allows sequentially buying low and selling high volatility.

Correlated Volatility Assets: Positive Vomma return potential improves when volatility correlates across related asset classes allowing capitalising in multiple markets.

Uncorrelated Volatility : Vomma options exhibit lower returns as convexity opportunities are more sporadic with Disjoint volatility across assets.

Volatility Skew Changes: Variable Vomma benefits from volatility skew changes as different curve points gap in volatility performance over time.

Positive Vomma options perform best when implied volatility starts low but trends higher over the holding period. Sideways low volatility dampens Vomma upside. But volatility means reversion and convexity across correlated markets enhance returns.

What are some common misconceptions or challenges associated with Vomma?

The biggest common misconception or challenge related to vomma is that high Vomma options are not inherently better. Vomma must be aligned with volatility expectations. Overpaying for high Vomma that is never realised is destructive. Here are nine more typical myths and difficulties around vomma in options trading.

Vomma Directly Increases Option Value: It does not directly increase the option’s price – only indirectly through vega while positive Vomma benefits from volatility spikes.

Vomma Decay Always Lowers Price: Vega decay from high Vomma does not necessarily mean the option is decreasing in total value, only sensitivity.

Vomma Is Easy to Exploit: Turning this into profitable strategies requires skill in volatility forecasting and risk management while Vomma quantifies convexity.

Vomma Scalping is Low Risk: Attempts to quickly trade Vomma spikes contain substantial model risks and volatility gap exposures.

Vomma Replaces Traditional Greeks: Vomma provides supplemental insights but does not replace foundational Greeks like delta, gamma, theta.

Negative Vomma is Always Bad: Negative Vomma has uses in vega hedging and reducing volatility drag in low volatility environments.

Vomma Is the Same as Volga: Volga specifically measures convexity in relation to the underlying price rather than volatility.

Vomma Divergences Guarantee Arbitrage: Apparent Vomma mispricings persist without the ability to properly hedge or capitalise on the difference.

Vomma Is Easy to Isolate: Vomma trades contain influences from other Greeks that complicate pure volatility convexity exposures.

Successfully incorporating Vomma into options trading requires nuanced volatility modelling, disciplined risk management, and accounting for its interactions with other Greeks. Vomma provides useful supplemental signals but has its own complexities.

What is the difference between Vomma and Volga?

The main difference between Vomma and Volga lies in what they measure. Vomma measures the sensitivity of an option’s delta to changes in implied volatility. It indicates how responsive the option’s delta will be to shifts in the underlying’s expected volatility. Options with high positive vomma have deltas that increase dramatically when volatility rises.

Volga, on the other hand, measures the sensitivity of an option’s vega to changes in implied volatility. Vega refers to the amount an option’s price moves when the underlying’s volatility changes. A high positive volga conveys that an option will experience significant price changes as its vega increases in high volatility environments.